KOMIYA Atsushi

KOMIYA Atsushi

Software engineer in Tokyo.

Java で最速の乱数生成器を目指す: (1) 正規乱数生成器

TL;DR: Java の java.util.Random#nextGaussian() や java.util.concurrent.ThreadLocalRandom のそれよりも 3 倍 以上速い正規乱数生成器 (正規分布に従う乱数生成器) を実装してみたよ、というお話です。

(Header photo by NJR ZA )

はじめに

ここ最近、お仕事的な何かで強化学習っぽい機能を実装したり、現実世界のとある問題を単純なモデルに置き換えてシミュレーションをぶん回してみる機会がちょこちょことあるのですが、そのような機能やシミュレータを実装しようとするときに「それなりの品質の乱数を とにかく速く 吐き出してくれる乱数生成器があると便利なんだけどなあ…」ということを時々思っています。

今の仕事で利用することの多い Java (or JVM 上の言語) では、Java 7 以降の標準クラスライブラリで提供されている java.util.concurrent.ThreadLocalRandom クラスが速度的にかなり優秀であるため、一様乱数だけを必要とするケースであれば、このクラスで満足いく速度は得られます (このあたりの話は過去にとある勉強会でお話したことがあるので、よろしければそのときの 資料 をご参照ください)。

その一方でケースとしてはそう多くないけれども、ときには正規分布に従う乱数が必要であったり、はたまた母数 α、β が状況に応じて常に変化しうるベータ分布からランダムサンプリングしたいんだよ、みたいなこともあったりします。前者の正規分布については Random#nextGaussian() メソッドが用意されているものの、速度的に十分満足できるかというとそうでもなくて、後者のベータ分布に至ってはそもそも機能的に標準クラスライブラリでは提供されていません。

このような場合はもはや (Java の標準クラスライブラリ以外の) 外部のライブラリに頼るしかなく、現時点では Apache Commons Math を選択するのがベストなのではないかと思われます。

この Commons Math では、メルセンヌツイスターなどのわりと高品質な乱数生成器の提供をはじめとし、豊富な確率分布の実装とそれらの確率分布からの乱数生成機能 (ランダムサンプリング) を提供しているという点において、とても重宝できます (もちろん、乱数生成以外の機能も充実しています)。ただし、確率分布からの乱数生成機能が速度的にイケてるかというと実はそうでもなくて、 Sampling from a ‘BetaDistribution’ is slow とか More efficient sample() method for ZipfDistribution とかを見てわかるように、意外と速度性能が悪かったりすることが間々あります (Issue 的には fixed になっているので、現在は解消されているかと思いますが…)。

そういうわけで、Java の世界における乱数生成器はその速度性能面で改善の余地があると思い、最速の乱数生成器の開発を目指してみようと思い立ちました。

正規乱数の生成アルゴリズムを選択する

何はともあれ、まず最初のターゲットは「正規乱数 (正規分布に従う乱数)」とします。

正規乱数は、一様分布や正規分布 以外 の確率分布における乱数生成アルゴリズムにおいて、一様乱数と同様に基礎的な乱数としてよく利用されます (具体例には Marsaglia と Tsang によるガンマ分布の乱数生成アルゴリズム があります)。そのため、正規乱数の生成速度を向上させることがその他の確率分布における乱数生成の速度性能を向上させることにもつながります。

さて、正規分布から乱数を生成するアルゴリズムとして何が一番適切なのかというと、現時点では Ziggurat アルゴリズム 択一ではないかと考えています。今回の乱数生成器の実装に際して「計算機シミュレーションのための確率分布乱数生成法」という書籍を主に参考にしているのですが、この書籍の p.144 に掲載されている各種アルゴリズムの比較においても他のアルゴリズムより頭一つ抜きん出た性能を示しています。

Ziggurat アルゴリズムによる正規乱数の生成

Ziggurat アルゴリズムがどのようなものなのか、その詳細を理解するには、先ほど挙げた「計算機シミュレーションのための確率分布乱数生成法」を読むか、英語 Wikipedia での説明、もしくは論文 The Ziggurat Method for Generating Random Variables を読むのが早いかと思います。

ここではざっくりと Ziggurat アルゴリズムの概念を説明することにとどめます。

  • 乱数生成の対象となる確率分布を、n - 1 個の「長方形」と「確率分布の裾の部分」の合計 n 個の領域に分割する (下図参照)
    • すべての「長方形」と「確率分布の裾の部分」の領域は、その面積がそれぞれ等しくなるようにする
    • すべての「長方形」の領域は、元の確率分布を (裾の部分を除いて) すべてカバーするように、また上から順に積み重ねるように配置する
  • 乱数を生成する際は、まずは n 個の領域 (n - 1 個の長方形と 1 個の裾の部分) のいずれかを一様乱数をもとに選択する
  • 選択した領域が長方形か確率分布の裾かで、別々の処理をする
    • 選択した領域が長方形の部分であれば、その領域内で棄却採択法による乱数生成を試みる
      • 長方形の形状を活かすことで、確率密度関数の計算を回避することができる
    • 選択した領域が裾の部分であれば、その裾の部分から乱数を生成する

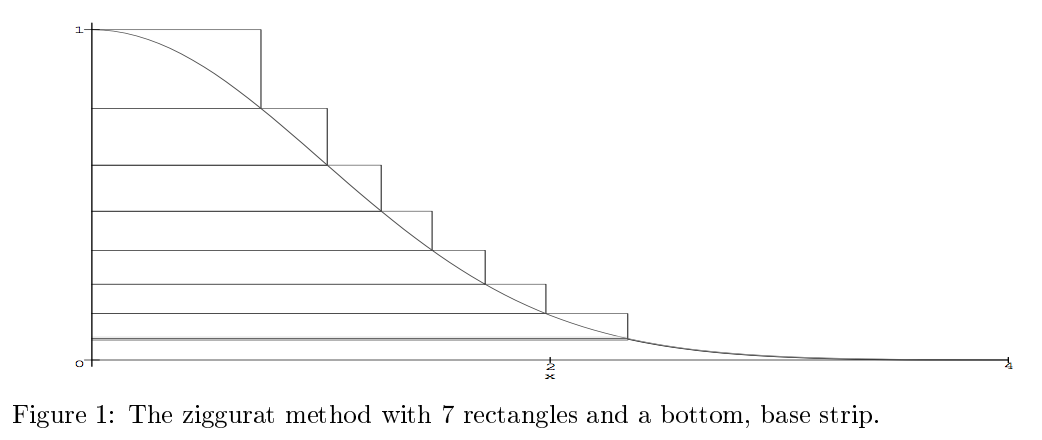Ziggurat (上記の図は The Ziggurat Method for Generating Random Variables より引用しています)

なお Ziggurat アルゴリズム自体は、正規分布以外の確率分布にも利用できるアルゴリズムです。今回は「計算機シミュレーションのための確率分布乱数生成法」に掲載されている正規乱数用のアルゴリズム 3.11, 3.12 をもとに、Java で実装をしました。

fast-rng: Fast random number generator for various distributions

そういうわけで、Ziggurat アルゴリズムによる正規乱数の Java 実装 (を含む乱数生成ライブラリ) を JCenter にて公開しています。

  • https://bintray.com/komiya-atsushi/maven/fast-rng

使い方は README.md にあるとおりで、Maven や Gradle などを使うのであれば、まず (1) Maven リポジトリ http://dl.bintray.com/komiya-atsushi/maven を追加し、続いて (2) 依存関係に group: biz.k11i, name: fast-rng を追加する必要があります。

正規乱数の生成は次のコードのように、(1) 一様乱数を生成する java.util.Random のオブジェクトを用意し、(2) biz.k11i.rng.GaussianRNG インタフェースを実装したクラスのインスタンスである GaussianRNG.FAST_RNG オブジェクトもしくは GaussianRNG.GENERAL_RNG を利用し、(3) GaussianRNG#generate(Random) を呼び出して正規乱数を生成する、という手順になります。

import biz.k11i.rng.GaussianRNG;

import java.util.Random;
import java.util.concurrent.ThreadLocalRandom;

public class GaussianRngDemo {
    public static void main(String[] args) {
        double mean = 0.0;
        double m2 = 0.0;

        // 一様乱数を生成する Random オブジェクトを用意する
        Random random = ThreadLocalRandom.current();

        final int N = 100000;
        for (int i = 0; i < N; i++) {
            // Random#nextLong() が返却する乱数の各ビットが独立であるなら、
            // GaussianRNG.FAST_RNG に置き換えることができる
            double r = GaussianRNG.GENERAL_RNG.generate(random);

            // 生成した乱数の平均と分散をオンラインで計算していく
            int n = i + 1;
            double delta = r - mean;
            mean += delta / n;
            m2 += delta * (r - mean);
        }

        double variance = m2 / (N - 1);

        // 平均は 0.0 ぐらい、分散は 1.0 ぐらいになるはず
        System.out.printf("mean = %.3f, variance = %.3f%n", mean, variance);
    }
}

上記のとおり、GaussianRNG の実装ではその内部に一様乱数を生成する機能を有しておりません。 GaussianRNG#generate(Random) で渡される Random オブジェクトの Random#nextLong() および Random#nextDouble() メソッドを呼び出して整数値 / 浮動小数点値の一様乱数を生成し、それを正規乱数の生成に利用しています。

GaussianRNG が提供する二つの実装 GaussianRNG.FAST_RNG, GaussianRNG.GENERAL_RNG はそれぞれ「計算機シミュレーションのための確率分布乱数生成法」のアルゴリズム 3.11, 3.12 に相当します。なお同書籍にも記載があるとおり、アルゴリズム 3.11 は整数値の一様乱数がビット独立でない場合には適していないため、そのような一様乱数を生成する Random オブジェクトを利用する場合には GaussianRNG.GENERAL_RNG を利用することをおすすめします。

パフォーマンス検証

さて、この Ziggurat アルゴリズムによる正規乱数の生成がどれくらいの速度パフォーマンスになるのかを、jmh でベンチマークをとって確認してみましょう。

今回の比較対象は次の 6 つになります。

  • FAST_RNG(java.util.Random)
    • 正規乱数の生成は FAST_RNG を利用
    • 一様乱数の生成は java.util.Random を利用
  • FAST_RNG(ThreadLocalRandom)
    • 正規乱数の生成は FAST_RNG を利用
    • 一様乱数の生成は ThreadLocalRandom を利用
  • GENERAL_RNG(java.util.Random)
    • 正規乱数の生成は GENERAL_RNG を利用
    • 一様乱数の生成は ThreadLocalRandom を利用
  • GENERAL_RNG(ThreadLocalRandom)
    • 正規乱数の生成は GENERAL_RNG を利用
    • 一様乱数の生成は java.util.concurrent.ThreadLocalRandom を利用
  • java.util.Random
    • java.util.Random#nextGaussian() を利用
    • ベンチマーク内で一つの java.util.Random オブジェクトを共有して利用する
  • ThreadLocalRandom
    • ThreadLocalRandom#nextGaussian() を利用

(Commons Math の正規乱数生成の実装は JDK と同じ Polar 法を利用していることと、スレッドセーフではないので今回の比較対象からは外しています)

シングルスレッドでの性能

まずはシングルスレッドで乱数生成した場合のパフォーマンスを確認してみます。

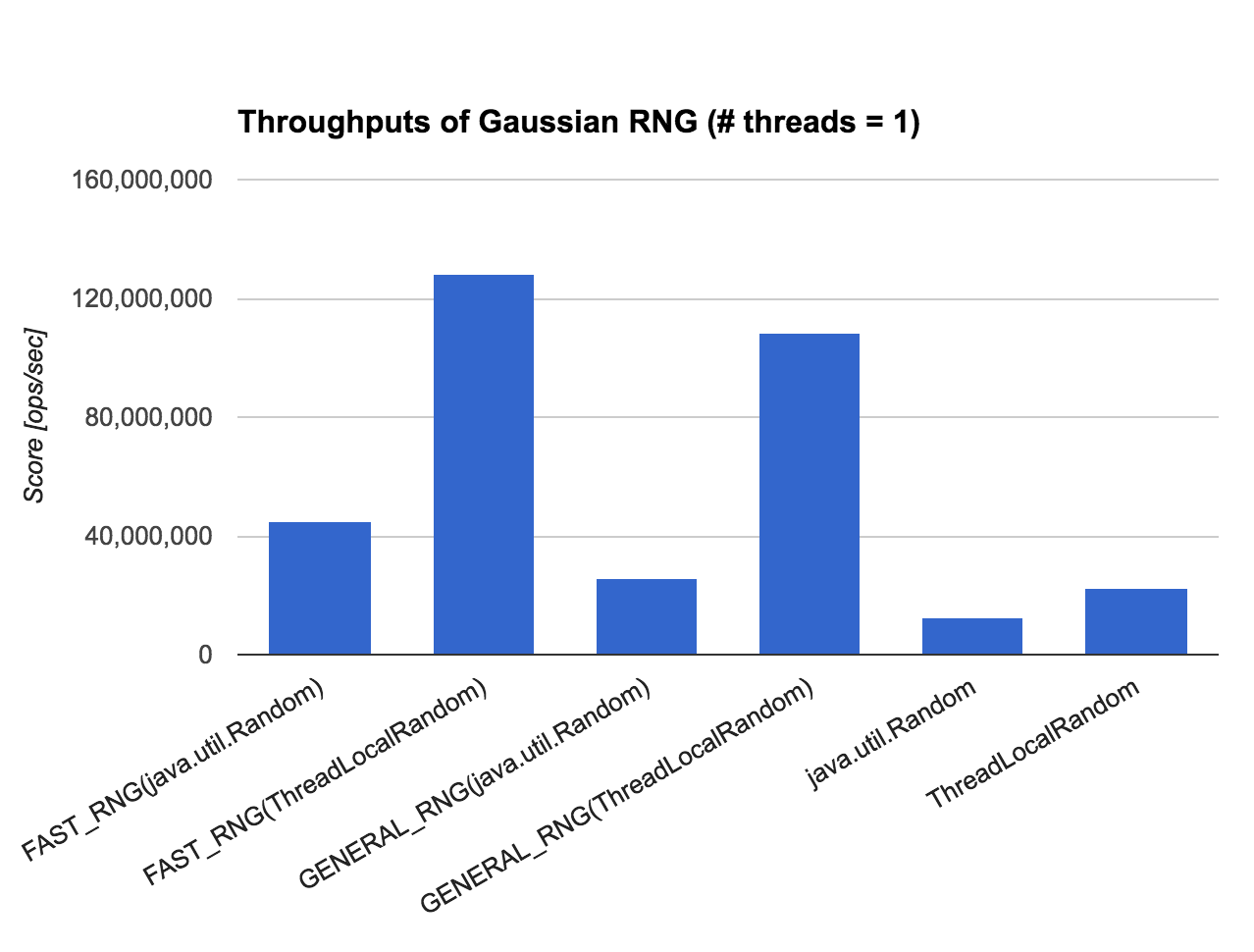
Throughputs of Gaussian RNG (# threads = 1)

ご覧のとおり、Ziggurat アルゴリズム & ThreadLocalRandom の組み合わせが圧倒的なパフォーマンスを叩き出しています。Java 標準で最速の ThreadLocalRandom#nextGaussian() と比較しても、5 倍近くのパフォーマンスが出ています。Random#nextGaussian() と比較すると 8 倍以上ですね。

ただ、FAST_RNG(java.util.Random) と FAST_RNG(ThreadLocalRandom) の二つを比較して分かるとおり、Ziggurat アルゴリズムで正規乱数を生成する場合であっても一様乱数の生成パフォーマンスが十分に速くなければ、それに引きずられて正規乱数の生成は遅くなってしまうことがわかります。

マルチスレッドでの性能

続いて、複数のスレッド上で並行して正規乱数を生成してみることにしましょう。 GaussianRNG はスレッドセーフとなるように実装しているので、一様乱数の生成がマルチスレッド環境下で効率的に動くのであれば、正規乱数の生成パフォーマンスもスケールしてくれるはずです。

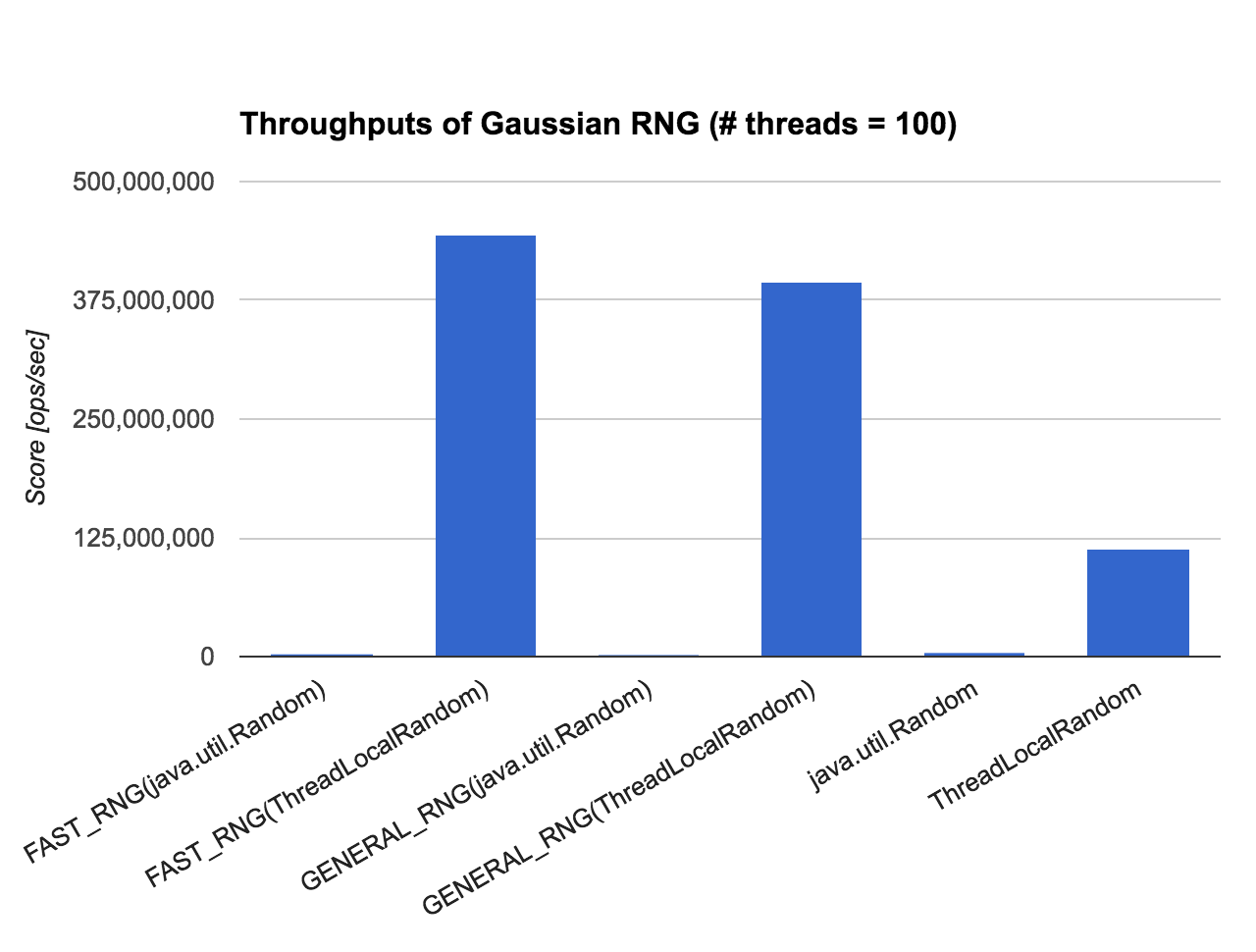
Throughputs of Gaussian RNG (# threads = 100)

結果は上記のとおり、一様乱数の生成に ThreadLocalRandom を使えば問題なくスケールしてくれます (その一方で、java.util.Random を利用すると結果は散々なものになります)。なお ThreadLocalRandom との性能差は 3.5 倍程度と若干その差は縮んでいます。

まとめ

今回は Java の正規乱数を高速に生成する Ziggurat アルゴリズムを実装し、Java 標準の正規乱数の生成機能 (特に ThreadLocalRandom) と比較をしました。その結果、シングルスレッドの場合で 5 倍以上、複数スレッドの場合でも 3 倍以上効率的に正規乱数を生成できるようになりました。

なお fast-rng は今回の正規乱数 (標準正規分布) に限らず (ゆっくりペースではありますが) これからも様々な確率分の乱数生成器を実装していくつもりでいます。

You may also enjoy