KOMIYA Atsushi

Software engineer in Tokyo.

TL;DR: ガンマ分布に従う乱数生成器を Java で実装し、Commons Math の実装と比較して 最大で約 16 倍 (任意の形状パラメータの乱数を生成する場合) の速度効率を達成しましたよ、というお話です。

(Header image: Mundhenk at en.wikipedia)

ガンマ分布に従う乱数生成の実装方法Permalink

これまで 正規分布に従う乱数生成、指数分布に従う乱数生成 をそれぞれ Java で実装してきましたが、今回はガンマ分布に従う乱数生成を Java で実装してみます。

ガンマ分布 は、形状パラメータ k>0 と スケールパラメータ θ>0 (もしくは形状パラメータ α=k と比率パラメータ β=1/θ) の 2 つのパラメータを持ち、その確率密度関数は次の式で表されます。

f(x)=xk−1e−x/θΓ(k)θk

ガンマ分布の形状パラメータ k は、下図のとおり確率密度関数の形状に影響を与えます (いずれもスケールパラメータは θ=1 です)。

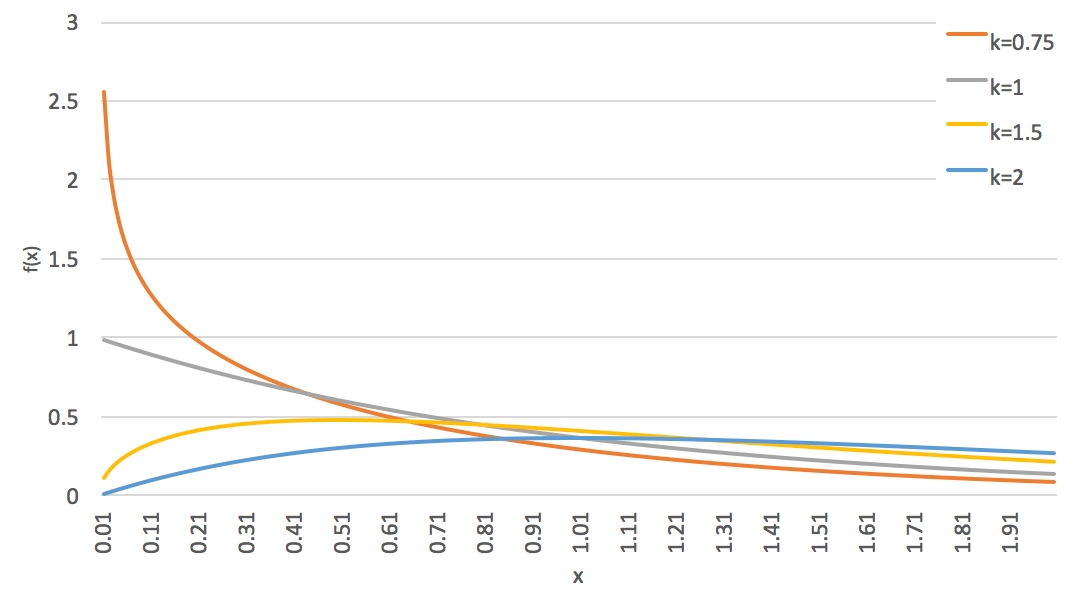
Gamma distribution

ガンマ分布に従う乱数生成では主に、スケールパラメータ θ=1 の標準ガンマ分布 Gamma(k,1) からの乱数生成を考えます。 スケールパラメータ θ が 1 以外の場合の乱数は、標準ガンマ分布に従う確率変数 X∼Gamma(k,1) に θ を乗じた確率変数 Y=θX がガンマ分布 Gamma(k,θ) に従うことを利用して、標準ガンマ分布から生成した乱数に θ を乗じることで得られます。

また、ガンマ分布に従う乱数の生成では、形状パラメータが 0<k≤1 の場合と k>1 の場合とで適用できうるアルゴリズムが異なります。 そのため、形状パラメータの値に対して k≤1 かどうかで条件分岐をして、利用するアルゴリズムを切り替える実装にする必要があります。

なお、今回実装するガンマ分布の乱数生成器は、「同一のパラメータで大量の乱数を生成する」ケースよりも、「都度異なるパラメータを指定して乱数を生成する」ケースで最適な速度効率になることを目指しています。 ガンマ分布の乱数生成アルゴリズムはその多くにおいて、形状パラメータ k に依存した何らかの 初期化ステップ を有していますが、今回はこの 初期化ステップ のオーバーヘッドも考慮してベンチマークを測定し、また乱数生成アルゴリズムを選定しています。

様々な乱数生成アルゴリズムPermalink

ガンマ分布に従う乱数生成器を Java で実装するにあたって、まずは候補となりうる乱数生成アルゴリズムを列挙してみます。ガンマ分布における主要な乱数生成アルゴリズムは「ガンマ乱数の生成方法について」1 にベンチマーク込みでまとめられているので、あわせてこちらをご覧いただくことをおすすめします。

  • 0<k≤1 の場合
    • Ahrens-Dieter (GS) 2
    • Best 3
    • Liu-Martin-Syring 4
  • k>1 の場合
    • Ahrens-Dieter (GD) 5
    • Schmeiser-Lal (G4PE) 6
    • Minh 7
    • Marsaglia-Tsang 8
    • Wilson-Hilferty approximation 9

それぞれのアルゴリズムの特徴について、以下簡単に触れます (アルゴリズムの詳細は各論文をご覧ください)。

Ahrens-Dieter (GS)Permalink

わりと古典的かつ簡素なアルゴリズムながら、さまざまな言語・ライブラリ (R の rgamma(), Commons Math など) で実装実績があります。初期化ステップにて数学関数を利用していないため初期化のオーバーヘッドが小さく、また棄却法のループ内で呼び出される数学関数も (実装にもよりますが) pow() が 1 回、log() と exp() がそれぞれ 0~1 回、合計 2 回と少ないのが特徴です。

BestPermalink

前述した Ahrens-Dieter (GS) と同程度に簡素なアルゴリズムです。Ahrens-Dieter (GS) と比較して棄却率の面で優れていますが、初期化ステップで sqrt(), exp() をそれぞれ呼び出す必要があり、初期化のオーバーヘッドが若干大きめとなります。

棄却法のループ内では pow(), exp(), log() がそれぞれ 0~1 回の呼び出し回数となりますが、圧搾法によって数学関数の呼び出しを避けるようにしているので、数学関数の呼び出し回数は 1 回のループあたり 1~2 回となります。

Liu-Martin-SyringPermalink

上記 2 つのアルゴリズムと比較して、ごく最近に提案されたアルゴリズムです。形状パラメータが k<0.3 と小さい場合において、前述の 2 つより優れた棄却率となります。一方で、棄却法のループ内で log() を 1 回、exp() を 3~4 回と数学関数を多数呼び出し、また一様乱数も 2~3 回生成するため、速度効率はそれほど期待できないものと思われます。

R による実装 rgamss() があります。

Ahrens-Dieter (GD)Permalink

R の rgamma() (k>1 の場合) や RANLIB の GENGAM の実装で使われているアルゴリズムです。 後述する Schmeiser-Lal (G4PE) や Minh には及ばないものの、その他のアルゴリズムと比較して乱数生成のステップが多いため、その実装は規模が大きめかつ複雑になります。

なお、このアルゴリズムは乱数生成ステップにおいて正規分布に従う乱数を一つ、指数分布に従う乱数を一つ以上生成します。そのため、それぞれの乱数生成器の速度性能がこのアルゴリズムの速度性能を左右することがあります。

Schmeiser-Lal (G4PE)Permalink

今回取り上げる k>1 の場合のアルゴリズムの中では、最も実装が複雑になるアルゴリズムです。 初期化ステップでは exp() および log() を 2~4 回呼び出すため、そのオーバーヘッドが大きくなることが予想されます。その後の棄却法のループ内には条件分岐が大量に存在し、また一様乱数の生成回数も 1~3 回となります。

MinhPermalink

Schmeiser-Lal (G4PE) のアルゴリズムと同程度に複雑なアルゴリズムです。Weka の RandomVariates#nextGamma(double) の実装で使われています。

このアルゴリズムも Schmeiser-Lal (G4PE) と同じく、初期化ステップにて exp() および log() を 3~4 回呼び出すことから相当のオーバーヘッドが生じるものと思われます。また棄却法のループ内も条件分岐が大量に存在します。

Marsaglia-TsangPermalink

今回取り上げる k>1 の場合に適用できるアルゴリズムの中では、最も単純なアルゴリズムになります。 numpy.random.gamma や Commons Math の実装に使われています。 初期化ステップでは sqrt() を 1 回、棄却法のループ内で log() を 0~2 回呼び出します。 また、棄却法のループ内では一様乱数に代わって正規分布に従う乱数を都度一つ生成するため、(ループ内の処理が単純なだけに) その乱数生成の速度性能がこのアルゴリズム全体の速度性能を大きく左右することになります。

なお、Marsaglia-Tsang のアルゴリズムが提案された論文において、0<k≤1 の場合の乱数を k>1 のアルゴリズムを用いて生成する方法が紹介されています。具体的には、0<k≤1 の場合の乱数を直接生成する代わりに Gamma(k+1,θ) に従う乱数 X と一様乱数 U∼unif(0,1) を生成し、XU1/k が Gamma(k,θ) に従うことを利用します。この方法を利用することで、k>1 のアルゴリズムによるガンマ分布に従う乱数生成に加え、一つの一様乱数、そして 1 回の pow() を呼び出すだけで 0<k≤1 の場合の乱数を生成することができます。この方法は特に、k>1 の乱数生成アルゴリズムの速度効率がよく、また一様乱数の生成が高速である場合に効果的に働きます (さらに k=1/2 の場合は XU2 となり、 pow() の呼び出しが不要になります)。

Wilson-Hilferty approximationPermalink

この Wilson-Hilferty の近似は厳密にはガンマ分布に従う乱数生成のアルゴリズムではなく、 χ2 分布を正規分布で近似する式に過ぎません。しかし「ベータ乱数生成法の改善に関する考察」10 にもあるとおり、この近似式を元に、次の式で正規分布 N(0,1) に従う乱数 Z からガンマ分布 Gamma(k,1) に従う乱数 X を生成できます。

X=k(1−19k+√19kZ)3

なお、この式で生成される乱数 X はあくまでも Gamma(k,1) に 近似的に従う だけなので、生成される乱数はガンマ分布とは厳密には異なる分布となることに注意が必要です。特に k が小さい場合に実際のガンマ分布との乖離が大きくなるため、ある程度大きな k の場合にこの近似アルゴリズムを使うのがよいと考えられます。具体的には k≥50 であれば、仮説検定を利用したテストケースを余裕でパスするぐらいの品質の乱数を生成できるようになります。

各種アルゴリズムの比較Permalink

さて、これまでに挙げてきたガンマ分布に従う乱数生成のアルゴリズムについて、その速度性能を評価してみましょう。

今回は、一様乱数の生成に Commons Math における Mersenne Twister の実装 MersenneTwister と JDK の ThreadLocalRandom を利用して、それぞれベンチマークをとってみます。また、形状パラメータを 0.05~0.9 (0.05~0.1, 0.1~0.9) / 1.0 / 2.0~10.0 / 50.0~10000.0 の間で変化させた場合ごとに結果をまとめることにします。

なお、以下に挙げる図における略称とアルゴリズムの対応は次のようになります。

略称 アルゴリズム
AD (GS) Ahrens-Dieter (GS)
AD (GD) fast Ahrens-Dieter (GD)
正規分布 / 指数分布に従う乱数生成にそれぞれ GaussianRNG.FAST_RNG, ExponentialRNG.FAST_RNG を利用
AD (GD) general Ahrens-Dieter (GD)
正規分布 / 指数分布に従う乱数生成にそれぞれ GaussianRNG.GENERAL_RNG, ExponentialRNG.GENERAL_RNG を利用
LMS Liu-Martin-Syring
MT.fast Marsaglia-Tsang
正規分布に従う乱数生成に GaussianRNG.FAST_RNG を利用
MT.general Marsaglia-Tsang
正規分布に従う乱数生成に GaussianRNG.GENERAL_RNG を利用
SL (G4PE) Schmeiser-Lal (G4PE)
WH.fast Wilson-Hilferty
正規分布に従う乱数生成に GaussianRNG.FAST_RNG を利用
WH.general Wilson-Hilferty
正規分布に従う乱数生成に GaussianRNG.GENERAL_RNG を利用

では、結果を見ていきましょう。

形状パラメータ k<1 の場合Permalink

まずは一様乱数生成器に Mersenne Twister を利用した場合の結果を見てみます。

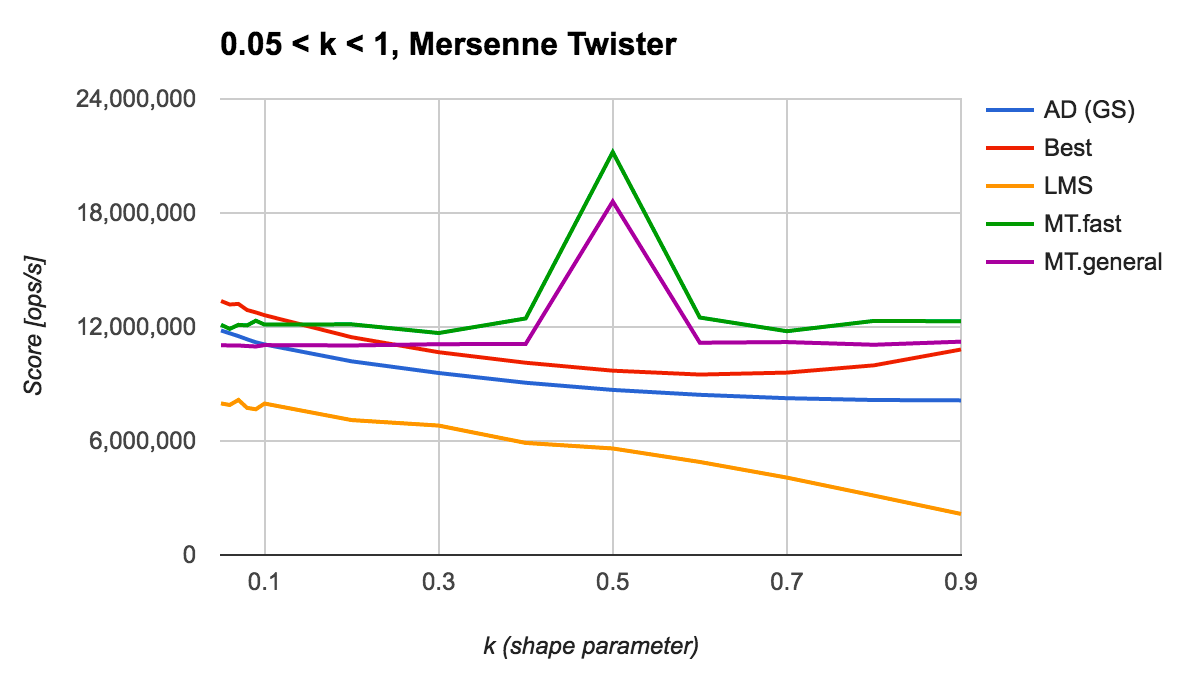
k <= 1 Mersenne Twister

上記の図より、それぞれのアルゴリズムの傾向は次のようになります。

  • Marsaglia-Tsang は (k=0.5 は例外として) k にほとんど左右されず安定して高い水準の速度性能を達成できている
    • k=0.5 で速度性能が突出して良くなっているのは、pow(u, 2) を呼び出す代わりに u * u で置き換えているため
  • Liu-Martin-Syring, Ahrens-Dieter (GS) は k が大きくなるに連れて速度性能が悪化していく
  • Best は k が 0 もしくは 1 に近い場合に速度性能がよい
    • k が 0.6~0.7 あたりで一番性能が落ち込む

アルゴリズム同士で比較をすると、終始性能がよいのは Marsaglia-Tsang, 一方で k が 0 に近い場合、特に k≤0.1 の場合に着目すると、Best が一番よいと言えるでしょう。

続いて、一様乱数生成器に ThreadLocalRandom を利用した場合の結果を見てみます。

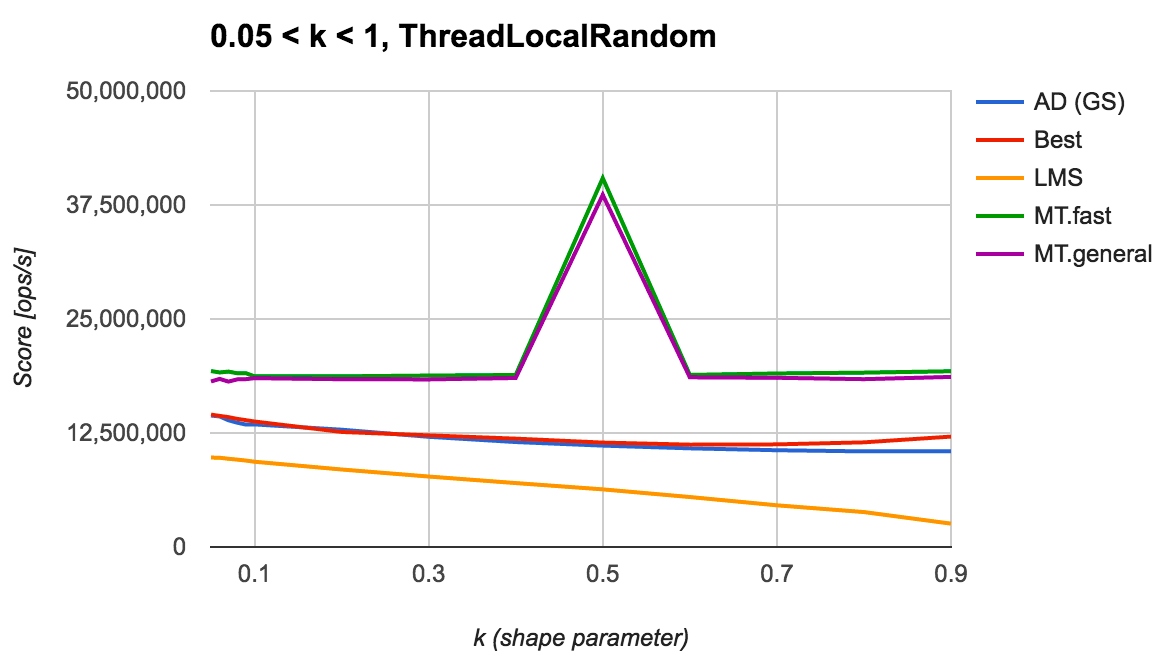
k <= 1 ThreadLocalRandom

Mersenne Twister のときとは異なり、Marsaglia-Tsang が終始最高性能を達成できています。 この結果より、一様乱数生成器自体が高速であることを期待できるならば、Marsaglia-Tsang のアルゴリズムを選ぶのがよいと言えそうです。

形状パラメータ k=1 の場合Permalink

次に、k=1 の場合の結果を見ていきます。 ここではガンマ分布 Gamma(1,1) が指数分布 exp(1) となることを利用して、指数分布に従う乱数生成器 ExponentialRNG.FAST_RNG, ExponentialRNG.GENERAL_RNG も加えてベンチマークを測定しています (一様乱数の生成器には Mersenne Twister を利用。ThreadLocalRandom の結果も同傾向)。

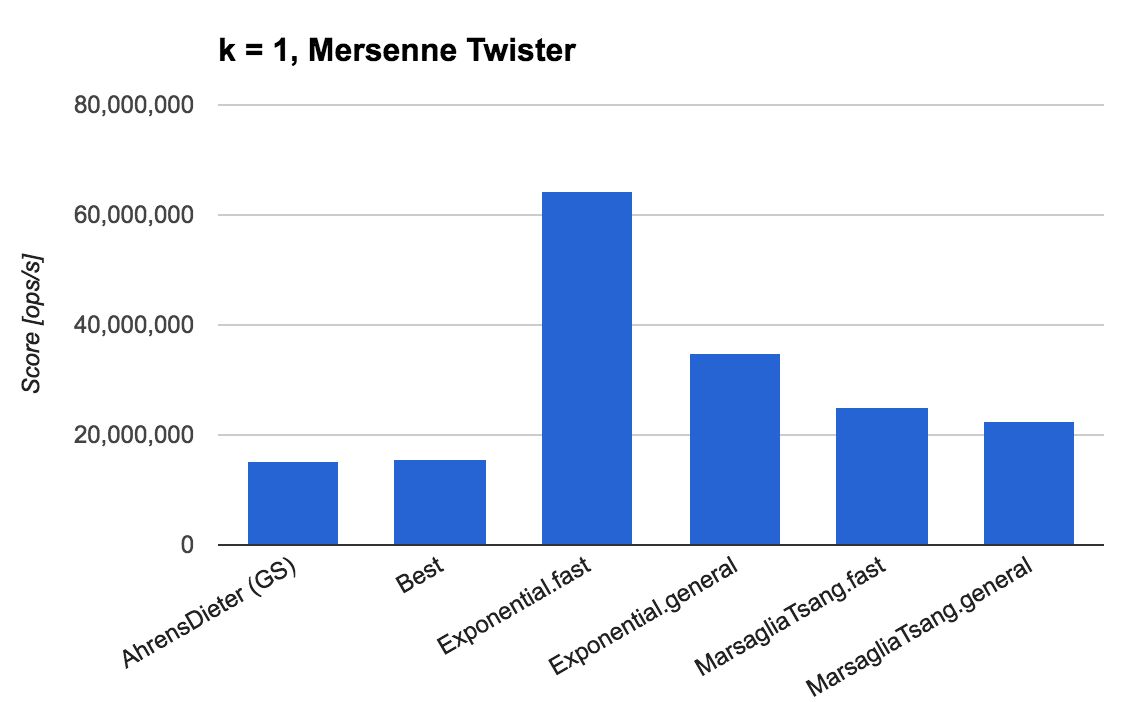
k = 1 Mersenne Twister

これまでに紹介した「ガンマ分布に従う乱数生成アルゴリズム」の中では Marsaglia-Tsang が最もよい速度性能を達成しています。しかし、Ziggurat アルゴリズムを用いて実装された ExponentialRNG の方がより優れた速度性能となることから明らかなように、k がちょうど 1 となる場合は指数分布からの乱数生成で置き換えるのがよいでしょう。

形状パラメータ 1<k≤10 の場合Permalink

続いて、k>1 ではあるけど、その値が比較的小さい (具体的には 10 以下の) 場合の結果を見てみます (一様乱数の生成器には Mersenne Twister を利用。ThreadLocalRandom の結果も同傾向)。

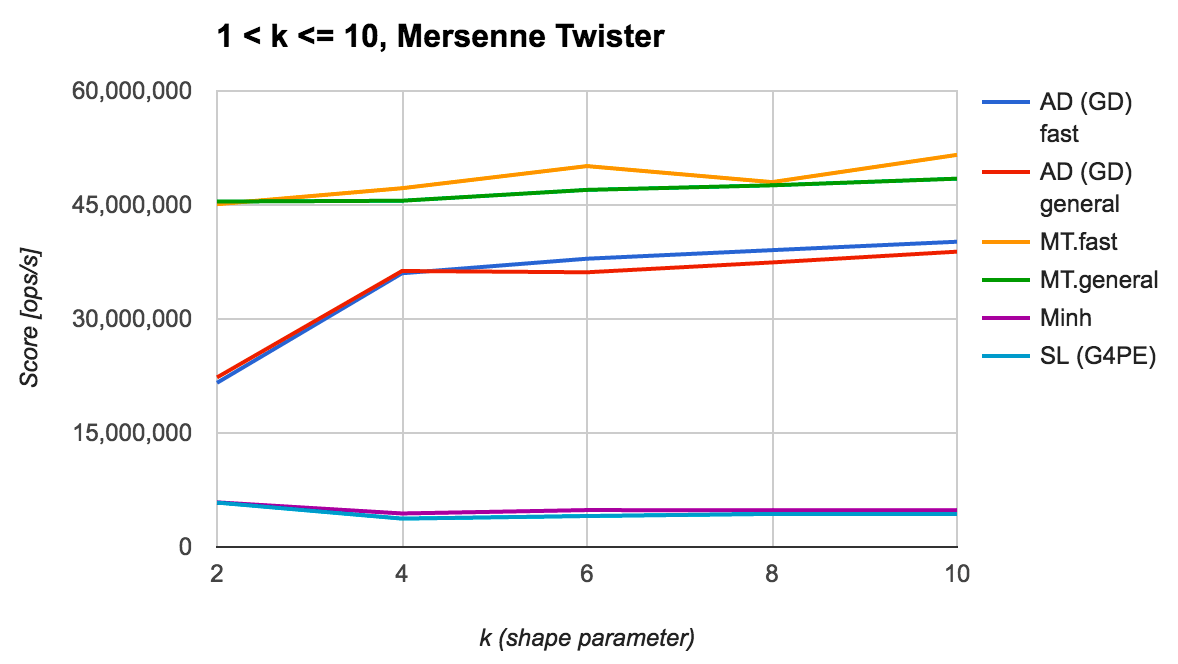
k > 1 Mersenne Twister

上記の図から、Marsaglia-Tsang が他より頭一つ抜きん出た速度効率を達成していることがわかります。 また、Ahrens-Dieter (GD) は今回のアルゴリズムの中では凡庸な性能であるものの、k が大きくなるにつれて速度性能が改善する傾向にあることにも注意が必要です。 一方で、Minh と Schmeiser-Lal (G4PE) の速度性能は上記二つと比較してかなり低迷しており、この結果だけを見るに採用は難しそうに思えます。

k がより大きな値になった場合の Ahrens-Dieter (GD) の性能は気になりますが、少なくとも k≤10 程度のケースにおいては Marsaglia-Tsang のアルゴリズムの優位性が揺らぐことはないでしょう。

形状パラメータ k≥50 の場合Permalink

最後に k が比較的大きな値となる場合の結果を見てみます (一様乱数の生成器には Mersenne Twister を利用。ThreadLocalRandom の結果も同傾向)。

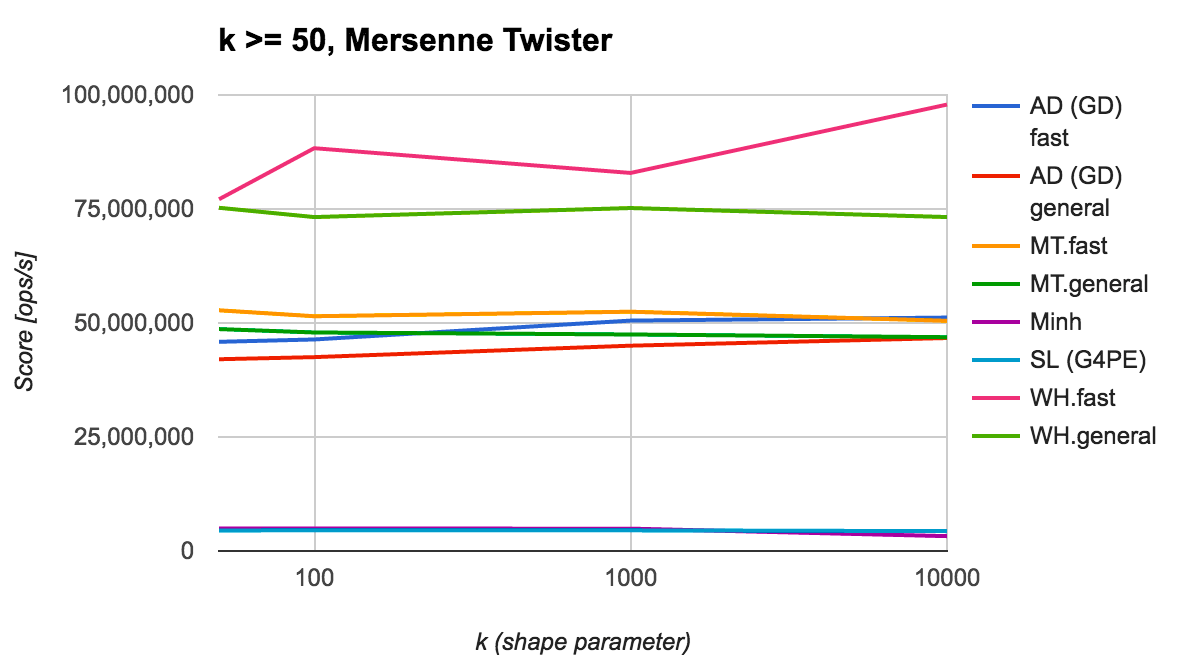
k >= 50 Mersenne Twister

k が 50 以上になれば Wilson-Hilferty の近似式による乱数生成が利用できるようになりますが、その性能は上記から明らかなように、とても効率がよいことがわかります。 Ahrens-Dieter (GD) の性能は k=10000 近辺で Marsaglia-Tsang に追いつくものの、Wilson-Hilferty の近似式の性能には到底敵いません。

この結果より、k≥50 であれば Wilson-Hilferty の近似式に基づいてガンマ分布に従う乱数を生成するのが最適と言えるでしょう。

fast-rng におけるガンマ分布の乱数生成アルゴリズムPermalink

前述した各種アルゴリズムのベンチマーク結果より、fast-rng の実装では 0.1.4 より、GammaRNG.FAST_RNG, GammaRNG.GENERAL_RNG それぞれの実装アルゴリズムを次のように選定しています。

  • GammaRNG.FAST_RNG
    • k<1 の場合: Marsaglia-Tsang w/ GaussianRNG.FAST_RNG
    • k=1 の場合: ExponentialRNG.FAST_RNG
    • 1<k<50 の場合: Marsaglia-Tsang w/ GaussianRNG.FAST_RNG
    • k≥50 の場合: Wilson-Hilferty approximation
  • GammaRNG.FAST_GENERAL_RNG
    • k≤0.3 の場合: Best
      • 一様乱数生成器に低速な実装を指定された場合でも、それなりの速度性能を維持することを目的に採用する
    • 0.1<k<1 の場合: Marsaglia-Tsang w/ GaussianRNG.FAST_RNG
    • k=1 の場合: ExponentialRNG.FAST_RNG
    • 1<k<50 の場合: Marsaglia-Tsang w/ GaussianRNG.FAST_RNG
    • k≥50 の場合: Wilson-Hilferty approximation

Commons Math との比較Permalink

前述した fast-rng のガンマ分布の乱数生成器が Commons Math のそれと対比してどれくらいの速度効率となるのかを、改めてベンチマークを計測して確認してみます。

今回は (1) 形状パラメータを固定して繰り返し乱数生成する場合と、(2) 任意の形状パラメータごとに 1 つの乱数生成する場合に分けて性能を測定しています。また先程の乱数生成アルゴリズムのベンチマークと同様に、一様乱数の生成に MersenneTwister と ThreadLocalRandom の 2 つを利用してみます。

(1) 形状パラメータを固定して繰り返し乱数生成する場合Permalink

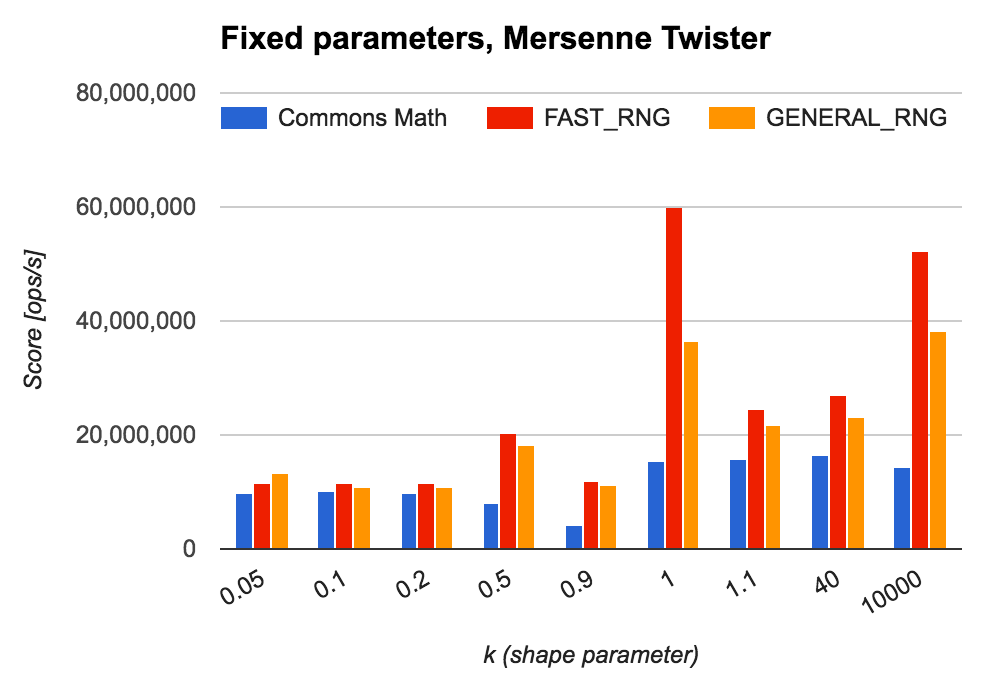
Mersenne Twister を利用して同じ形状パラメータで乱数生成を生成した場合は、下図より、

  • k<1 ではあまり大きな差は生じない
    • 特に k が 0 に近い場合は Commons Math と比較しても 1.05~1.17 倍程度の速度性能に落ち着く
    • ただ k が 1 に近づくにつれて Commons Math の実装の速度性能は低下するので、相対的な性能差は徐々に開いていく
  • k>1 では、Commons Math と比較して 1.4~3.6 倍の速度性能となる
    • 特に k が大きな値 (k≥50) になった場合は、Wilson-Hilferty の近似アルゴリズムによってより性能差が大きくなる

といった傾向が見られることがわかります。

Fixed parameters, Mersenne Twister

一方で ThreadLocalRandom を利用した場合は、その性能差がより顕著になることが下図より見て取れます。

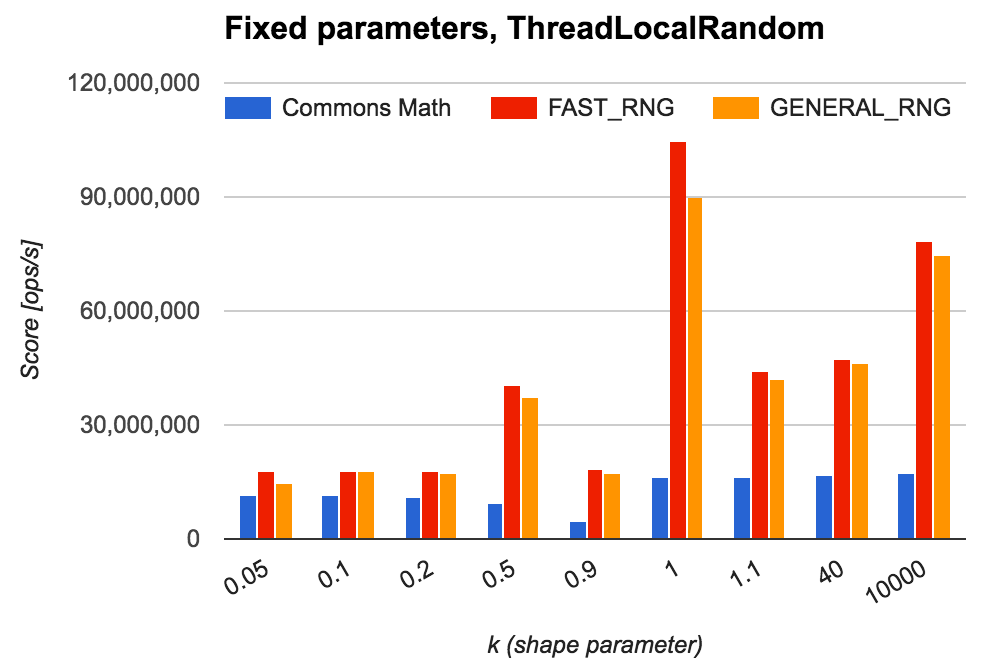
Fixed parameters, ThreadLocalRandom

(2) 任意の形状パラメータごとに 1 つの乱数生成をする場合Permalink

このベンチマークでは、指数分布 exp(10) からサンプリングした 10,000 個の数値を形状パラメータとして順繰りに利用し、必要なオブジェクトの生成から乱数を実際に生成するまでの処理をその測定対象としています。

Mersenne Twister, ThreadLocalRandom それぞれの結果を以下に示します。

(Mersenne Twister における結果) Score [ops/s] 性能比
Commons Math 1,953,763 -
fast-rng (FAST_RNG) 21,165,270 10.43
fast-rng (GENERAL_RNG) 17,789,078 8.77
(ThreadLocalRandom における結果) Score [ops/s] 性能比
Commons Math 2,028,923 -
fast-rng (FAST_RNG) 33,938,186 16.73
fast-rng (GENERAL_RNG) 31,380,037 15.47

どちらの結果も Commons Math と比較して 8 倍以上の速度性能を達成しています。この結果は、Commons Math における乱数生成において、確率分布のオブジェクト生成 new GammaDistribution(shape, scale) の処理時間を含んでいることが影響しています。

fast-rng は、任意のパラメータに対する乱数生成が最適になるように不必要なオブジェクト生成が生じないような設計・実装がなされています。 その一方で、Commons Math における確率分布からの乱数生成機能は「確率分布」が提供する機能の一つとして位置づけられていることもあり、任意の形状パラメータが与えられた場合の乱数生成には都度「確率分布」のオブジェクト生成が要求されます。

Java におけるオブジェクト生成の時間的なコストは皆が知るとおり、数学関数の呼び出しなどよりも遥かに大きなものとなりうるため、乱数生成アルゴリズムもさることながらオブジェクト生成の機会を減らすことも時には必要となります。

まとめPermalink

今回はガンマ分布に従う乱数生成アルゴリズムについて、その速度性能を検証しました。今回の検証結果は fast-rng 0.1.4 の実装に反映されています (ガンマ分布に従う乱数生成の機能そのものは fast-rng 0.1.1 より提供していましたが、0.1.4 で速度改善を果たした、ということになります)。

利用ケース次第では Commons Math と比較して最大で 16 倍程度の速度性能を達成することができます。Java におけるガンマ分布の乱数生成で速度的にお困りのことがあれば、ぜひ fast-rng を一度お試しください :smile:

参考文献Permalink

  1. 谷崎久志. “ガンマ乱数の生成方法について.” 国民経済雑誌 197.4 (2008): 17-30. ↩

  2. Ahrens, Joachim H., and Ulrich Dieter. “Computer methods for sampling from gamma, beta, poisson and binomial distributions.” Computing 12.3 (1974): 223-246. ↩

  3. Best, D. J. “A note on gamma variate generators with shape parameter less than unity.” Computing 30.2 (1983): 185-188. ↩

  4. Liu, Chuanhai, Ryan Martin, and Nick Syring. “Efficient simulation from a gamma distribution with small shape parameter.” Computational Statistics (2016): 1-9. ↩

  5. Ahrens, Joachim H., and Ulrich Dieter. “Generating gamma variates by a modified rejection technique.” Communications of the ACM 25.1 (1982): 47-54. ↩

  6. Schmeiser, Bruce W., and Ram Lal. “Squeeze methods for generating gamma variates.” Journal of the American Statistical Association 75.371 (1980): 679-682. ↩

  7. Minh, Do Le. “Generating gamma variates.” ACM Transactions on Mathematical Software (TOMS) 14.3 (1988): 261-266. ↩

  8. Marsaglia, George, and Wai Wan Tsang. “A simple method for generating gamma variables.” ACM Transactions on Mathematical Software (TOMS) 26.3 (2000): 363-372. ↩

  9. Wilson, Edwin B., and Margaret M. Hilferty. “The distribution of chi-square.” Proceedings of the National Academy of Sciences 17.12 (1931): 684-688. ↩

  10. 石井陽真, et al. “ベータ乱数生成法の改善に関する考察.” 日本経営工学会論文誌 66.4 (2016): 372-375. ↩

You may also enjoy

LexoRank とは何か？

世の中に転がってる LexoRank の日本語解説記事がどうにも腑に落ちない内容だったので、この記事をしたためることにしました。