Java で最速の乱数生成器を目指す: (4) ベータ分布に従う乱数
今回は commons-math3 の BetaDistribution#sample() より 最大で 4 倍以上速い ベータ分布に従う乱数生成器を実装しましたよ、というお話です。
(Header image: Dr. J. Rodal / Wikipedia)
ベータ分布に従う乱数の生成方法Permalink
ベータ分布は Wikipedia の説明 にあるように、二つの形状パラメータ α>0 と β>0 を持ち、その確率変数は x∈[0,1] となる確率分布です。
書籍「計算機シミュレーションのための確率分布乱数生成法」では、このベータ分布に従う乱数の生成方法として、ガンマ分布に従う乱数を利用する方法を紹介しています。具体的には、 二つのガンマ分布に従う乱数 r1∼Gamma(α,1), r2∼Gamma(β,1) を用いて、 x=r1r1+r2 としてベータ分布 Beta(α,β) に従う乱数 x を生成します。
この方法は、(ガンマ分布の乱数生成アルゴリズムを除けば) 実装がとてもシンプルであり、ベータ分布のパラメータ α,β の値がどのような値であっても適用できるという特徴があります。また、ガンマ分布からの乱数生成さえ十分に高速であれば、ベータ分布の乱数生成もそこそこの速さが期待できると考えられます。NumPy では実際に、この方法をベータ分布の乱数生成に利用しています。
これ以外にも、ベータ分布に従う乱数の生成アルゴリズムは論文 Evaluation of Beta Generation Algorithms で列挙されているように数多く存在します。ここでは、同論文で列挙されている各種アルゴリズムについて、速度性能の観点でよい性能が期待できそうな以下のアルゴリズムに着目してみることにしました。
- Jöhnk
- Jöhnk, M. D. “Erzeugung von betaverteilten und gammaverteilten Zufallszahlen.” Metrika 8.1 (1964): 5-15.
- NumPy では、α≤0 もしくは β≤0 の場合にこのアルゴリズムを利用しています
- Cheng’s BB / BC
- Cheng, Russell CH. “Generating beta variates with nonintegral shape parameters.” Communications of the ACM 21.4 (1978): 317-322.
- R の rbeta() や Java の commons-math3 で、BB / BC のアルゴリズムが利用されています
- Sakasegawa’s B00 / B01 / B11
- B4PE
- BPRS
なおアルゴリズムによっては、パラメータ α,β が特定の範囲の値の場合にのみ適用可能であることに注意が必要です。上記したそれぞれのアルゴリズムを適用できるパラメータ α,β の範囲を以下に示します。1
| Algorithm \ parameter | Case 1: α<1, β<1 |
Case 2: α<1<β |
Case 3: α>1, β>1 |
|---|---|---|---|
| Jöhnk | ✓ | ✓ | ✓ |
| BC | ✓ | ✓ | - |
| BB | - | - | ✓ |
| B00 | ✓ | - | - |
| B01 | - | ✓ | - |
| B11 | - | - | ✓ |
| B4PE | - | - | ✓ |
| BPRS | - | - | ✓ |
ベンチマーク (1): パラメータごとに最適なアルゴリズムを探るPermalink
ここからは具体的に、上記した 3 つのケースにおいて適用可能なアルゴリズムの速度性能をベンチマークで評価し、最適なアルゴリズムを探っていきます。 なお、表に挙げたアルゴリズムに加えて、二つのガンマ分布に従う乱数を用いる方法も性能評価の対象としています。
ケース 1: α<1, β<1Permalink
まずは、ケース 1 に適用できるアルゴリズムについて、いくつかの α,β の組み合わせごとに性能測定してみました。 ベンチマーク結果は下表のとおりです (単位は 1 秒あたりの乱数生成個数。TGV は、二つのガンマ分布に従う乱数を用いる方法 を示しています)。
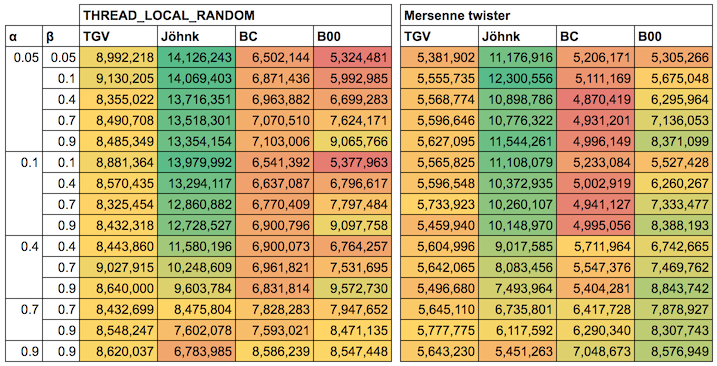
この結果より、
- TGV
- パラメータによらず一貫して安定した速度性能となる
- 一方で、一様乱数生成器の速度に性能が左右されやすい
- Jöhnk
- 二つのパラメータのいずれか一方でも 0 に近いほど、速度性能はよい
- 逆に、二つのパラメータが 1 に近づくにつれて速度性能が劣化していく
- Sakasegawa’s B00
- 二つのパラメータがともに 0 に近い場合の速度性能は、明らかに悪い
- 反対に、二つのパラメータのうちいずれかでも 1 に近い場合は、速度性能は大きく改善する
- TGV ほど一様乱数生成器の速度に性能が左右されず、安定している
- Cheng’s BC
- 二つのパラメータがともに 1 に近い場合に、速度性能が最も良くなる
- ただいずれのアルゴリズムと比較しても、速度性能的な長所がない
ということがわかります。よって、α,β が 0 に近い場合は Jöhnk を、1 に近い場合は B00 を利用するのが得策と言えそうです。
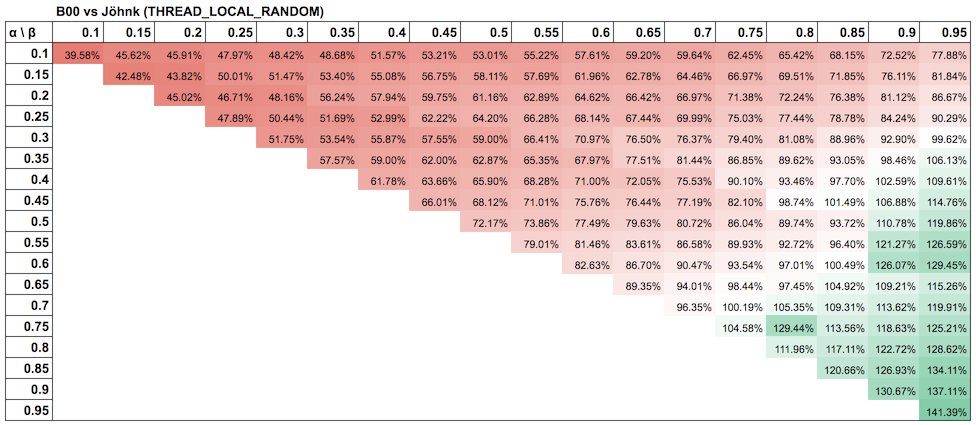
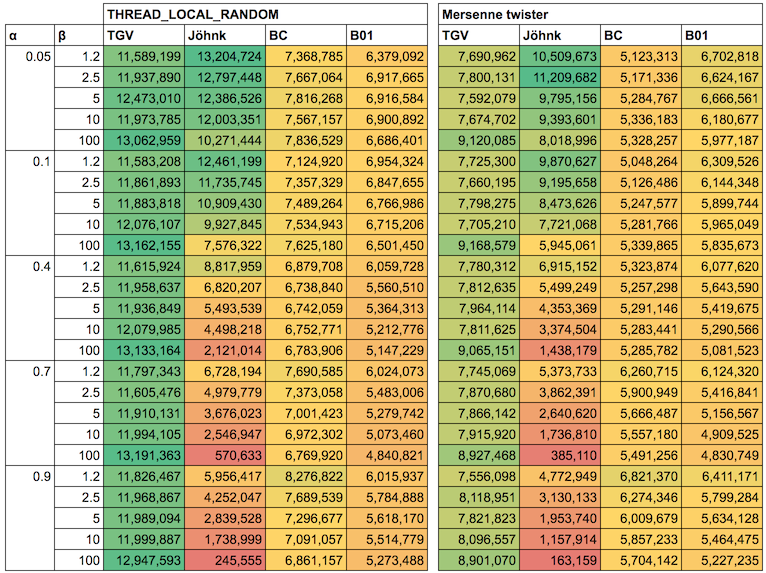
次は、具体的に α,β がどの値の場合に Jöhnk (もしくは B00) を使うべきか、その境界を決めることにします。今度は α,β ともに 0.05 刻みで変化させ、測定結果を「B00 の性能 / Jöhnk の性能」の割合で表現してみました。
以下は一様乱数の生成に ThreadLocalRandom を利用した場合の結果です。
こちらは Mersenne twister の結果です。
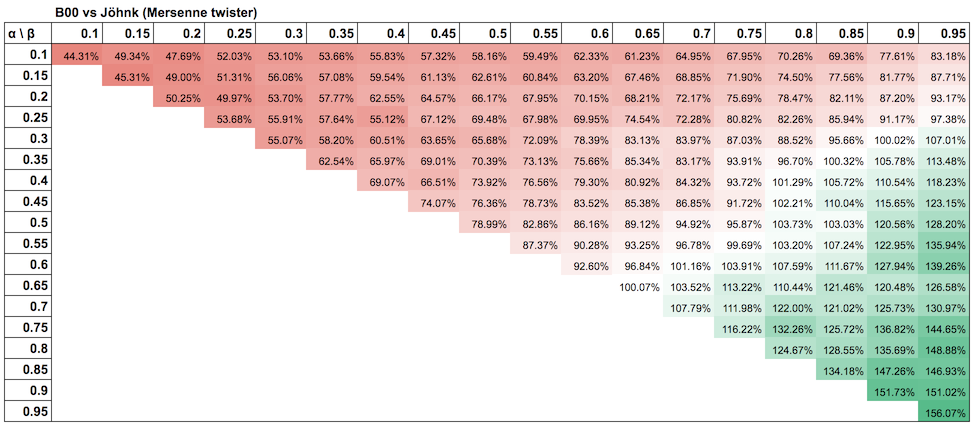
両者を参考に、α+β>1.5 となるパラメータの組み合わせにおいて B00 を利用し、それ以外は Jöhnk を利用することにします。
ケース 2: α<1<βPermalink
ケース 2 においても 1 のときと同様に、まずは適用可能なアルゴリズムの速度性能の比較をします。
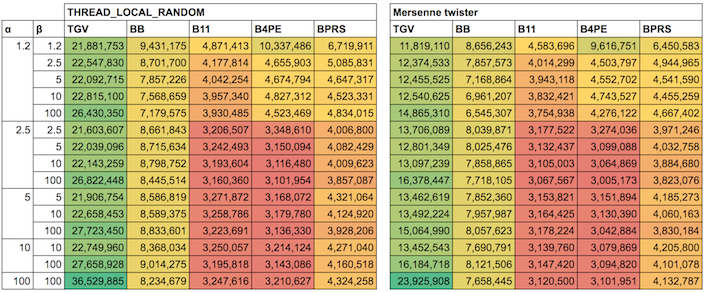
上記結果より、
- Cheng’s BC / Sakasegawa’s B01 はともに TGV に劣る
- Jöhnk は α,β がともに小さい値の場合に最良ではあるが、値が大きい場合は TGV に劣る
となり、これより α,β の値に応じて TGV と Jöhnk を切り替えるとよいことがわかります。
なおこれら二つのアルゴリズムを切り替えるパラメータの境界は、ケース 1 のときのような単純な一次式で表すことができません。そのため、α の値を 0.01 刻みで変化させつつ、それぞれの α の値においてアルゴリズムを切り替えるのに最適な β の値をパフォーマンスを実測しながら求めることにします。その結果をルックアップテーブルにすることで、アルゴリズムを切り替えるパラメータの境界を 1e-2 の精度に丸めた α を用いて表引きで決定できるようにします。
ケース 3: α>1,β>1Permalink
ケース 3 に適用可能なアルゴリズムの速度性能は以下のとおりです。
見てのとおり TGV が常に速く、このケースにおいては TGV 択一となります。
その他のケースPermalink
上記した 3 つのケースはいずれも、その区間が境界値 α=1, β=1 を含まない開区間となっています。これはベータ分布に従う乱数を生成するアルゴリズムの多くが α=1 もしくは β=1 のパラメータを取り扱えないことによります。そこでここでは、少なくともどちらかのパラメータが 1 になる場合の各ケースを考えていきます。
まず α=1, β=1 のケースを考えます。この場合は、ベータ分布の累積分布関数が Ix(1,1)=x となることから分かるとおり、一様分布からの乱数生成で置き換えることができます。
次に α≠1, β=1 のケースを考えます。このケースは厳密には α<1, β=1 と α>1, β=1 の二つが考えられますが、どちらのおいても、以下のいずれかが乱数生成アルゴリズムの有力な候補となります。
- ベータ分布の累積分布関数 Ix(α,1)=xα から逆関数法で求める (INV)
- この累積分布関数の逆関数は F−1(u)=u1α となる
- 二つのガンマ分布に従う乱数を用いる方法
- Jöhnk のアルゴリズム
これらの速度性能を比較した結果は以下のとおりです。

α<1, β=1 では、逆関数法が最も速度効率のよい方法になります。一方 α>1, β=1 では、α が小さい場合はわずかながら逆関数法が、α が大きい場合は、ガンマ分布からの乱数生成が効率的になる ことから TGV が速度効率のよい方法となります。
ベンチマーク (2): commons-math3 との比較Permalink
上記のベンチマーク結果を参考に、今回実装する乱数生成アルゴリズムは以下のように構成します。
- α=1, β=1
- 一様分布からの乱数生成で置き換える
- α≤1, β≤1
- 原則として Jöhnk を利用する
- α+β>1.5 の場合は、Sakasegawa’s B00 を利用する
- α<1, β=1 の場合は、逆関数法を利用する
- α=1, β<1 の場合も逆関数法を利用し、1−u1β とする
- α<1<β
- Jöhnk と二つのガンマ分布に従う乱数を用いる方法を利用する
- α≥1, β≥1
- 常に二つのガンマ分布に従う乱数を用いる方法を利用する
さて、このアルゴリズムと commons-math3 の BetaDistribution#sample() について、その速度性能を比較してみましょう。様々なパラメータ α,β を指定した場合に、速度性能がどれくらい違うのかを比較した結果が以下になります。
| Implementation \ Uniform RNG | Mersenne twister | ThreadLocalRandom |
|---|---|---|
| commons-math3 | 4,006,006 | 4,059,856 |
| BetaRNG.FAST_RNG | 13,003,885 | 19,075,616 |
| BetaRNG.GENERAL_RNG | 10,629,072 | 16,642,516 |
一様乱数の生成に Mersenne Twister を利用した場合だと最大 3.2 倍、ThreadLocalRandom であれば 4.7 倍ほどの速度性能の向上となりました。
まとめPermalink
今回はベータ分布に従う乱数を生成する各種アルゴリズムについて速度性能を検証し、その結果をもとに fast-rng 0.1.5 にてベータ分布の乱数生成器を実装しました。
ベータ分布に従う乱数は例えば、ベルヌーイ多腕バンディットにおける Thompson sampling での利用が考えられます。より具体的な例としては、Web 広告のクリエイティブ配信を CTR や CVR に基いて、Thompson sampling で最適化する問題が挙げられます。2
このクリエイティブ配信最適化は、各々のクリエイティブ i のインプレッション数 vi とクリック数 ci の実績値を基に生成される乱数 ri∼Beta(ci,vi−ci) について、その乱数が最大となるクリエイティブを選択する、という手順で実現できます。
Web 広告配信の世界では、広告リクエストが発生してから実際に広告を表示するまでのレイテンシをできる限り小さくすることが常に求められるため、処理が重くなりがちな確率分布からの乱数生成を少しでも高速化することには価値があると言えるでしょう。