Java / Commons Math で一変数の関数を最適化する
滅多なことがなければ使うことはないだろうけど、Commons Math の BrentOptimizer クラスを使って一変数の関数を最適化 (最小化 or 最大化) する方法をメモしておきます。
一変数関数の連続最適化問題Permalink
このエントリで言及している「一変数関数1の連続最適化」とは具体的に何かというと、「一変数の関数 f(x) について、区間 l≤x≤h における関数の最大値 (もしくは、最小値) およびそのときの x を求める」ということに相当します。そして、この一変数関数の連続最適化問題を解く方法の一つとして、Brent 法が存在します。
Brent 法の実装は、FORTRAN によるものが netlib に fmin として存在しており、R の optimize() はこの FORTRAN 実装を C に翻訳したものを使っています。他には SciPy の scipy.optimize.brent で実装されており、今回利用する Commons Math の BrentOptimizer クラス はこの SciPy の実装を一部元にしているようです。
以降は、この BrentOptimizer クラスおよびその使い方について見ていきます。
BrentOptimizer クラスPermalink
Brent 法を使って、一変数の関数の最適化を実現するクラスです。具体的には、BrentOptimizer#optimize(OptimizationData...) メソッドで諸々のパラメータを指定して、最適化を実行します。このメソッドの呼び出しにおいて指定が必要となるパラメータは、以下のとおりです。
UnvariateObjectiveFunction(Javadoc)- 最適化対象となる目的関数を表します
- 後述する
UnvariateFunctionインタフェースのオブジェクトをこのクラスのオブジェクトで包みます
GoalType(Javadoc)- 最小化したいのか、それとも最大化したいのかを表します
- 最小化なら
GoalType.MINIMIZE、最大化ならGoalType.MAXIMIZEを指定します
SearchInterval(Javadoc)- 拘束条件 (x の区間) と初期値 (指定は任意) を表します
- この区間において目的関数が凸でないと、局所解に陥る可能性が生じます
MaxEval(Javadoc)- 目的関数を評価する回数に対する上限値を表します
- 目的関数が評価回数がこの上限値を超えると、例外が発生します
- 最適化が終了するわけではないことに注意が必要です
- 上限を設けたくない場合は、
MaxEval.unlimited()を指定します
BrentOptimizer クラスのコンストラクタでは、最適化結果の精度を左右する二つのパラメータ rel, abs を指定します。rel は Math.ulp(1d) * 2 以上の値を、また abs は 0 より大の値を指定する必要があります。
UnvariateFunction インタフェースPermalink
このインタフェースを extend して、最適化したい目的関数を実装します。例えば、目的関数が f(x)=x2 であれば、
new UnvariateFunction() {
@Override
public double value(double x) {
return x * x;
}
}
のように実装します。Java 8 以降で、かつ目的関数がわりと容易に記述できるのであれば、わざわざ匿名クラスにしなくともラムダ式で書いたほうがシンプルにできるでしょう。
最適化の例Permalink
例として、区間 [0,3] における f(x)=x3−3x2 の最小値を求めてみます2。この関数 f(x) はグラフで表すと次のような形状となります。
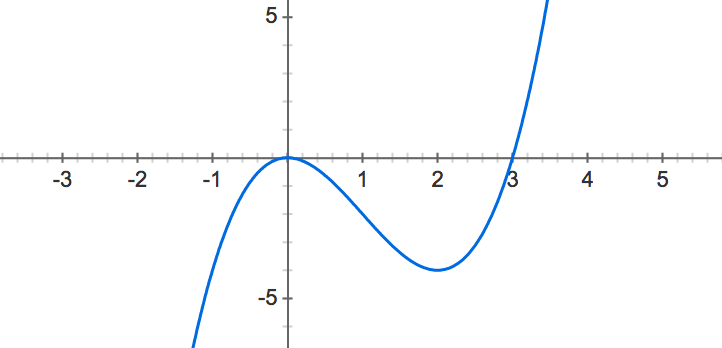
この最小化問題を BrentOptimizer を使って実装すると次のようになります。
import org.apache.commons.math3.optim.MaxEval;
import org.apache.commons.math3.optim.nonlinear.scalar.GoalType;
import org.apache.commons.math3.optim.univariate.BrentOptimizer;
import org.apache.commons.math3.optim.univariate.SearchInterval;
import org.apache.commons.math3.optim.univariate.UnivariateObjectiveFunction;
import org.apache.commons.math3.optim.univariate.UnivariatePointValuePair;
public class UnivariateOptimization {
public static void main(String[] args) {
UnivariatePointValuePair result = new BrentOptimizer(2 * Math.ulp(1d), Double.MIN_NORMAL)
.optimize(
new UnivariateObjectiveFunction(x -> x * x * x - 3 * x * x),
GoalType.MINIMIZE,
MaxEval.unlimited(),
new SearchInterval(0, 3.0)
);
System.out.println("minimum: " + result.getValue());
System.out.println("x: " + result.getPoint());
}
}
実行結果はこちら。
minimum: -4.000000000000002
x: 1.9999999930246806
ぴったり x=2 にはなりませんでしたが、厳密な解が必要でない状況で使う分にはこれで十分じゃないでしょうか。
