ベイズ統計の最高事後密度区間を Java で求める

ベイズ統計における「信用区間」の一つである最高事後密度区間 (Highest posterior density interval, HPDI) について、その区間を求める方法を調べて Java で実装してみたメモです。

最高事後密度区間とは？

そもそもの 最高事後密度区間 を自分自身がちゃんと理解していないので、まずは定義を確認しておきます。

Web 上の日本語文献だと「確率分布の密度が高い部分の n%」みたいなゆるふわな説明が多かったので、あえて Cross Validated の What is a Highest Density Region (HDR)? の回答 を参考にしてみると、その定義は以下のようになるようです。

確率変数 $X$ の確率分布 $P(X)$ について、その確率密度関数を $f(x)$ とする。この $f(x)$ に対し、値が $f_\alpha$ 以上となる $x$ の集合 $R(f_\alpha) = \lbrace x \ \vert \ f(x) \ge f_\alpha \rbrace$ を $100(1-\alpha)\%$ 最高事後密度区間 とする。

ここで $f_\alpha$ は $P(X \in R(f_a)) \ge 1 - \alpha$ を満たす最大の定数である。

このように文章で表現するとなかなかイメージが掴みづらいですが、これを単峰性の確率分布を例に (具体的にはベータ分布 $Beta(8,4)$) 図で表現すると

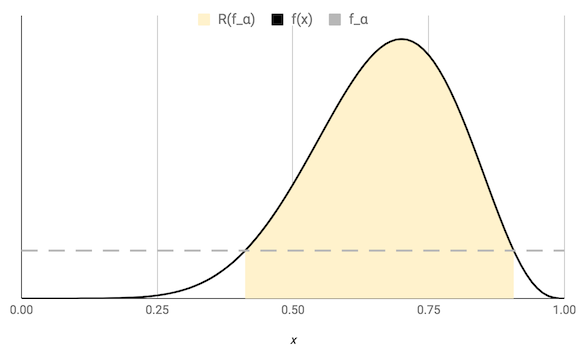
のようになります。つまりは、

• 区間内の確率密度が常に $f_\alpha$ 以上になる
• 逆に、区間外の確率密度は常に $f_\alpha$ 未満となる
• 区間内の確率は $1 - \alpha$ となる

これらの条件を満たす区間が 最高事後密度区間 であると言えます。

最高事後密度区間を Java で求める

さて、任意の 単峰性の確率分布 における最高事後密度区間をどのように求めるのかというと、これまた Cross Validated の Credible set for beta distribution の回答 に具体的な手順が紹介されています。

ここで紹介されているのは 一変数関数の最適化問題として解く 方法で、具体的には確率分布 $P(X)$ の累積分布関数を $F(x)$、また

\[y = F^{-1}(F(x) + 1 - \alpha) \tag{1}\]

としたとき、目的関数は次の式になります。

\[(f(y) - f(x))^2 + ((F(y) - F(x)) - (1 - \alpha))^2 \tag{2}\]

この目的関数を $x \in (-\infty, F^{-1}(\alpha))$ の区間で最小化することで得られる $x$ が最高事後密度区間の左端に、また式 $(1)$ に従って得られる $y$ が右端となります。

この手順を Java で実装するとなるとまず、一変数関数を最適化する手段を用意する必要があります。こちらは Java / Commons Math で一変数の関数を最適化する のエントリにあるように、Commons Math の BrentOptimizer を利用すれば一変数関数の最適化は実現できます。

後は、先の Cross Validated の回答にある R 実装を参考にしつつ Java で実装すればよいわけで、具体的な実装は次のようになります。

import org.apache.commons.math3.analysis.UnivariateFunction;
import org.apache.commons.math3.distribution.BetaDistribution;
import org.apache.commons.math3.distribution.RealDistribution;
import org.apache.commons.math3.optim.MaxEval;
import org.apache.commons.math3.optim.nonlinear.scalar.GoalType;
import org.apache.commons.math3.optim.univariate.BrentOptimizer;
import org.apache.commons.math3.optim.univariate.SearchInterval;
import org.apache.commons.math3.optim.univariate.UnivariateObjectiveFunction;
import org.apache.commons.math3.optim.univariate.UnivariatePointValuePair;

public class HighestPosteriorDensityInterval {
    private final double lowerBound;
    private final double upperBound;

    HighestPosteriorDensityInterval(double lowerBound, double upperBound) {
        this.lowerBound = lowerBound;
        this.upperBound = upperBound;
    }

    public double getLowerBound() {
        return lowerBound;
    }

    public double getUpperBound() {
        return upperBound;
    }

    public static HighestPosteriorDensityInterval calculate(RealDistribution distribution, double alpha) {
        Solver solver = new Solver(distribution, alpha);

        double lowerBound = solver.solve();
        double upperBound = solver.offset(lowerBound);

        return new HighestPosteriorDensityInterval(lowerBound, upperBound);
    }

    static class Solver implements UnivariateFunction {
        private static final double THRESHOLD = 1e-15;
        private static final MaxEval MAX_EVAL = new MaxEval(100);

        private final RealDistribution distribution;
        private final double alpha;

        Solver(RealDistribution distribution, double alpha) {
            this.distribution = distribution;
            this.alpha = alpha;
        }

        double solve() {
            UnivariatePointValuePair result = new BrentOptimizer(THRESHOLD, THRESHOLD)
                    .optimize(
                            GoalType.MINIMIZE,
                            new UnivariateObjectiveFunction(this),
                            MAX_EVAL,
                            new SearchInterval(
                                    distribution.getSupportLowerBound(),
                                    distribution.inverseCumulativeProbability(alpha),
                                    distribution.inverseCumulativeProbability(alpha / 2)));

            return result.getPoint();
        }

        double offset(double x) {
            double q = distribution.cumulativeProbability(x);
            return distribution.inverseCumulativeProbability(Math.min(q + 1 - alpha, 1));
        }

        @Override
        public double value(double x) {
            double y = offset(x);
            double d1 = distribution.density(y) - distribution.density(x);
            double d2 = (distribution.cumulativeProbability(y) - distribution.cumulativeProbability(x)) - (1 - alpha);
            return d1 * d1 + d2 * d2;
        }
    }
}

上記のクラスの利用方法は次のとおり。

public class HpdiDemo {
    public static void main(String[] args) {
        BetaDistribution distribution = new BetaDistribution(8, 4);

        HighestPosteriorDensityInterval interval = HighestPosteriorDensityInterval.calculate(distribution, 0.05);

        // 95% 最高事後密度区間 [0.412047441090850, 0.906627667219367] が出力される
        System.out.printf("[%.15f, %.15f]", interval.getLowerBound(), interval.getUpperBound());
    }
}