KOMIYA Atsushi

KOMIYA Atsushi

Software engineer in Tokyo.

Java で Rank9 を実装する

Xor+ filter を実装するために、ランク辞書の一種である Rank9 を Java で実装したメモです。

Rank9 とは？

Rank9 は、ビットベクトルに対する ランククエリ を定数時間で実現するランク辞書の一種です。提案論文は こちら。

この Rank9 は 2-layer で構成される典型的なランク辞書ではあるのですが、64 ビット CPU での処理に適した構成をとっています。具体的には以下の図に示すとおりで、

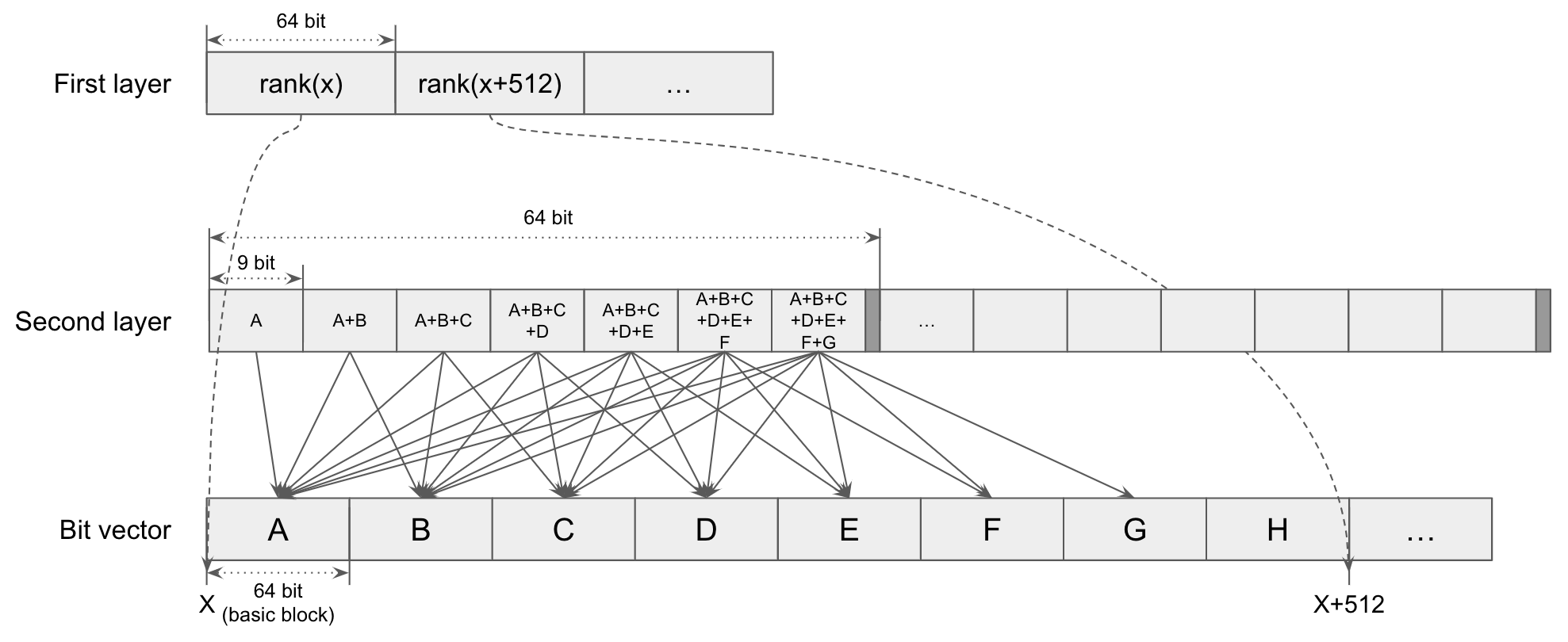
rank9

  • ビットベクトルを 64 ビットごとに区切り、それぞれを basic block として扱う
  • First layer では、 8 個の basic block (= 512 ビット) ごとのランク を 64 ビットで表現する
  • Second layer では、 連続する 8 個の basic block 内部における basic block ごとのランク (first layer のランクからの相対的なランクに相当する) を 9 ビットで表現する
    • ただし、最初の basic block のランクは常に 0 となるので省く
    • 残り 7 個の basic block のランクを、1 ビットのパディングとともに 64 ビットに詰めて表現する

となります。なお、上記の図では first layer と second layer を分離して表現していますが、 実装上はこれらの値を交互に織り込んで (すなわち interleaved に) 一つの配列で表現 します。この interleaved な構成により、ランクを求める際のキャッシュミスを最大 2 回に抑えられます1。

このランク辞書を用いて $i$ ビット目のランクを求める手順は、次のようになります。

  1. First layer と second layer から、一つ手前の basic block までのランクを求める
  2. ビットマスクとのビット積と POPCNT 命令 などを用いて、$i$ ビット目が含まれる basic block 内でのランクを求める2
    • 最近の Java3 であれば、Long.bitCount() メソッドを利用することで POPCNT 命令の利用が期待できる
  3. 1 と 2 の結果を合算して最終的なランクとする

この手順を具体的に Java のコードで表現するならば、例えば以下のようになるでしょう。

// それぞれ first layer, second layer, basic block を表す
long[] first;
long[] second;
long[] blocks;

public long rank(long i) {
    int blockIndex = (int) (i >>> 6);
    int tableIndex = (int) (i >>> 9);
    int shiftBits = 63 - (blockIndex & 0x7) * 9;
    long mask = (1L << (i & 0x3f)) - 1;

    return first[tableIndex]
            + ((second[tableIndex] >>> shiftBits) & 0x1ff)
            + Long.bitCount(blocks[blockIndex] & mask);
}

なお、second layer から 9 ビットの値で表現された 8 basic block 内のランクを抽出する処理では、「$i$ ビット目が存在する対象の basic block が、連続する 8 つの basic block のうち、最初の basic block に該当するか？」を判定する (すなわち条件分岐をする) 必要はなく、上記のように常に同じ単にビット演算を適用するだけで済みます。

小規模なビットベクトル向けのちょっとした最適化

先に示した論文における Rank9 では、first layer のランクの表現に 64 ビットの整数を用いていました。ゆえに Rank9 では、その長さが $2^{32}$ を超える (厳密には、ランクが $2^{32}$ を超える) ビットベクトルを取り扱うことができます。

このとき、ランク辞書の表現に要するビット数は、元のビットベクトルの長さを $n$ ビットとすると $0.25 n$ ビットとなり、元のビットベクトルに対して 25% のオーバーヘッドが生じることになります。

一方でアプリケーション次第にはなるのですが、実際に取り扱うビットベクトルの長さが $2^{32}$ を超えることがないのであれば、first layer のランクは 32 ビットの整数で表現することができます。この場合、ランク辞書の表現に要するビット数は $0.185 n$ ビットとなり、18.5% のオーバーヘッドに抑えることができます。ただしこの場合は first layer と second layer を interleaved な構成にするのが難しく、それぞれ別の配列で表現することになるため、キャッシュミスが最大 3 回となることに注意が必要です。

また、ビットベクトルの長さが同じく $2^{32}$ を超えないケースのさらなる別種として、first layer と second layer をそれぞれ 32 ビット値で表現しつつ、この 2 つを合わせて 64 ビットの値として取り扱う方法が考えられます。この場合のオーバーヘッドは 25% のままとなりますが、速度的に優位性があるか否かを後述するベンチマークで評価することにします。

ベンチマーク

計測条件

ここでは以下の条件に基づいて、Rank9 の具体的な各種実装の速度性能 (スループット, ops/ms) を計測することにします。

  • ビットの 0/1 が概ね半々の割合で含まれる、長さ $2^{30}$ のランダムなビットベクトルに対するランク辞書を用意する
    • ビットベクトルそのものに要するバイト数は 128MiB となる
    • ランク辞書に要するバイト数は、25% のオーバーヘッドであれば 32MiB、18.5% のオーバーヘッドであれば 24MiB となる
  • 上記のビットベクトル/ランク辞書に対して、都度ビットインデックスをランダムサンプリングしてランククエリを実行したときのスループットを計測する

今回速度性能を評価する Rank9 の実装は、以下の 4 つになります。

名称 オーバーヘッド 説明
RANK9_32 18.5% First layer を 32 ビットで表現し、second layer とは別の配列で表現する
RANK9_32_INTERLEAVED 25% First / second layer をそれぞれ 32 ビットで表現しつつ、1 つの 64 ビット整数でまとめて表現する
RANK9_64 25% First / second layer を別々の配列で表現する
RANK9_64_INTERLEAVED 25% 論文に基づくオリジナルの実装

計測結果

ベンチマークの計測に使ったコードは こちら です。結果は以下の通り。

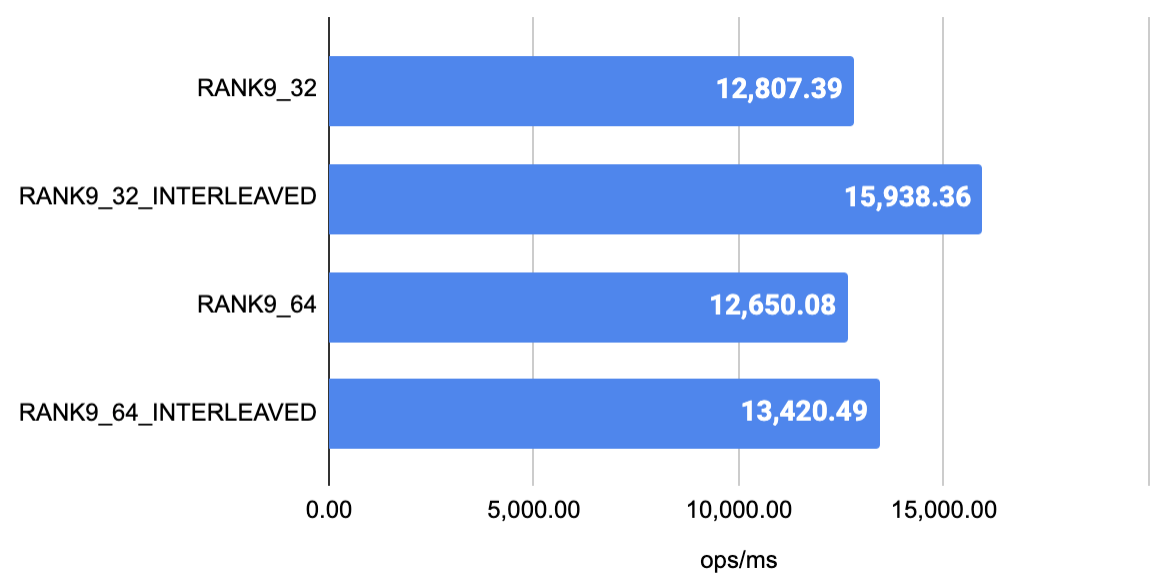
ベンチマーク結果

この結果をみて明らかなように、first layer と second layer を interleaved な構成にすることは速度性能にポジティブな影響を与え、また first / second layer それぞれを 32 ビットで表現して 64 ビットの数値で扱うことにより、さらなる速度性能の向上が見込めることがわかります。

一方で、first layer だけを 32 ビットで表現してオーバーヘッドを 18.5% に抑える実装は速度性能を犠牲にすることになるため、この実装の採用には慎重にならざるを得ないと考えられます。

まとめ

今回は Rank9 (およびその派生) を Java 実装し、その速度性能をベンチマークで評価してみました。ビットベクトルの大きさがそれほど大きくない場合は、オリジナルの Rank9 よりも 32 ビットで first / second layer を表現し、64 ビットの数値として保持する実装の方が優れていることがわかりました。

なおこの Rank9 が提案されたのは 2008 年頃と随分と昔であり、それ以降も様々なランク辞書が提案されていることから、今後はこの Rank9 をベースラインとし、引き続きそれぞれのランク辞書を実装して速度性能を評価してみることにします。

  1. 古典的な (interleaved ではない) 2-layer 構成のランク辞書だと、それぞれのレイヤを構成する配列へのアクセスで 1 回ずつ、またビットベクトルへのアクセスで 1 回、の合計で 3 回キャッシュミスが生じ得ます。 ↩

  2. POPCNT 命令が存在しない CPU の場合は、元論文にあるようなビット演算を用いたビットカウントを利用することになります。 ↩

  3. Java Bug Database JDK-6378821 を見るに、Java 1.6 時点で既に利用できたようです。 ↩

You may also enjoy