Java で最速の乱数生成器を目指す: (5) 0 以上 bound 未満の整数の乱数生成

java.util.Random#nextInt(int bound) 相当の乱数生成を高速化しました、というお話です。

TL;DRPermalink

• Nearly divisionless アルゴリズム (arXiv) を Java で実装してみたよ
• 色んな bound を取っ替え引っ替え指定するベンチマークで評価した結果、Java 8 の ThreadLocalRandom#nextInt(int bound) と比較して約 1.18 倍の高速化が期待できるよ
• fast-rng 0.2.0 に UniformRNGUtils として組み込んだ ので今すぐ使えるよ

Nearly divisionless アルゴリズムの特徴・性能Permalink

Nearly divisionless アルゴリズムは、0 以上 2L 未満の整数の一様乱数をもとに、0 以上 bound (=任意の上限値) 未満の整数の乱数を偏りなく生成するアルゴリズム の一種です。この手のアルゴリズムの利用用途としては例えば、歪みのない立方体のサイコロを振る操作のシミュレーションなどが挙げられるでしょう。

このアルゴリズムはその名が示すとおり、計算を工夫することでなるべく剰余演算をせずに目的の区間の乱数生成が行えるという特徴を有しています。除算や剰余演算は、加算・減算や乗算と比較すると未だに計算コストが高めな演算であるため、それを回避することができれば乱数生成の高速化が見込める、というわけです (アルゴリズムの詳細は後述します)。

その速度性能は、任意の上限値を 210 個用意して順繰りに指定するベンチマーク で評価した場合に ThreadLocalRandom#nextInt(int bound) と比較して、以下のグラフにあるように 約 1.18 倍の高速化が見込めるほどになっています (ThreadLocalRandom の結果は jdk のラベルで表しています)。

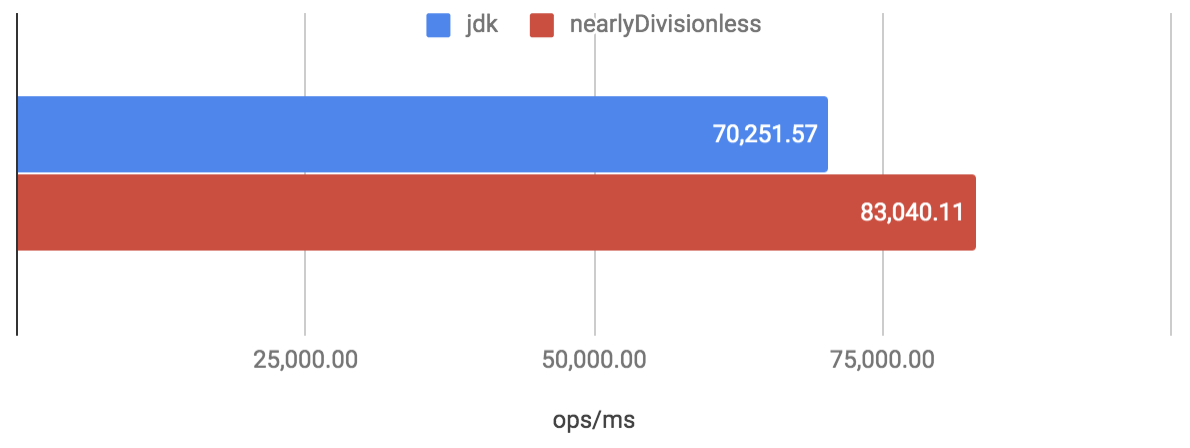
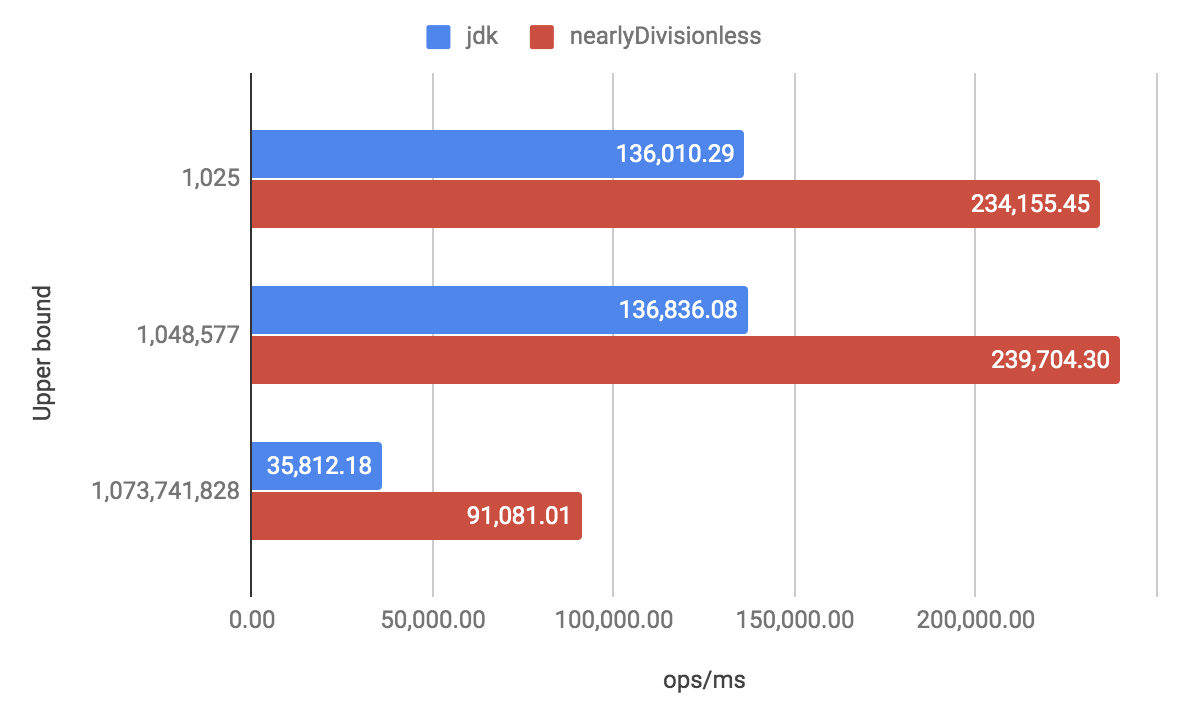
また、上限値を固定した場合のベンチマーク で評価した場合は、JDK 実装のアルゴリズムが特に苦手としている 230 を超えた上限値において約 2.54 倍の速度性能を達成しています。

アルゴリズム詳説Permalink

ここからは nearly divisionless アルゴリズムの詳しい説明をしていきます。

Nearly divisionless 以前のアルゴリズムPermalink

まず本題に入る前に、Random#nextInt(int bound) 相当の一般的な乱数生成アルゴリズムを考えていきましょう。

「0 以上の bound 未満の整数の乱数を生成する」という問題、より厳密に言い換えるならば「[0,2L) の区間の整数の一様乱数 r∼U([0,2L)) から、[0,n) の区間 (ただし 0<n<2L) の整数の一様乱数 r′∼U([0,n)) を生成する」問題は、ともするとシンプルに剰余演算 rmodn で解決できそうに思えます。しかし単に剰余演算を利用しただけでは、生成される整数それぞれの生起確率に偏りが生じる 結果を生み出しかねません。例えば n=⌊2L/3⌋×2 の場合を考えると、剰余演算のみで得られる乱数は 2L/3 付近を境にして、それより前と後の数値の生起確率に大きな偏りが生じる (2L/3 より前の数値の方が、それより後の数値よりも 2 倍の生起確率になる) ことになります。

この剰余演算による偏りの問題は、棄却法 を利用することにより解決できます。今回対象としている問題に対して棄却法を採用している実装例として OpenBSD の arc4random_uniform() を挙げると、この実装では一様分布 U([0,2L)) から生成した乱数のうち、[2Lmodn,2L) の区間に含まれる値だけを採択して目的の乱数生成に利用しています。最終的な乱数生成は GitHub 上の同実装のコードにあるようにただの剰余演算なのですが、U([0,2L)) から生成した乱数のうち 2Lmodn 未満の乱数を切り捨てることで実質的に利用できる乱数が 2L−(2Lmodn) 個に限られ、この個数が n でちょうど割り切れることで偏りのない乱数生成ができるようになります。

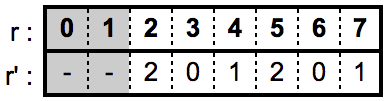
具体例として L=3, n=3 の場合について考えてみます。以下の図に示すとおり 、[23mod3,23) つまりは [2,8) の区間に含まれる乱数 r のみを採択して r<2 を棄却することにより、0, 1, 2 それぞれの数値の生起確率がすべて 1/3 になることがわかります。

そして、Java の Random#nextInt(int bound) や ThreadLocalRandom のそれも、アルゴリズムこそ違えど 棄却法を用いた実装 となっています。

この OpenBSD と JDK の実装は、必要となる剰余演算の回数に違いがあります。具体的には、OpenBSD の実装は、棄却回数に関わらず常に 2 回の剰余演算が必要となるのに対し、JDK の実装は棄却が生じなければ 1 回の剰余演算、棄却が生じるたびに +1 回の追加の剰余計算が生じます。この剰余演算の回数の違いにより、JDK の実装は特に棄却率が低くなる n において OpenBSD の実装よりも高速な乱数生成が期待できます。

剰余演算を避ける方法Permalink

上述したとおり、OpenBSD も JDK の実装もどちらも目的の区間内の乱数を生成するのに一回以上の剰余演算を必要しています。一方で nearly divisionless アルゴリズムは、状況次第では剰余演算を一回も行わず に、またその必要が生じても わずか一回の剰余演算だけ で目的の乱数を生成できます。この剰余演算が必要となる確率は n に依存しており、n が小さいほどその確率は小さく (つまりは剰余演算なしに乱数生成できることに) なります。

さて、この剰余演算を避けるアルゴリズムのポイントは、それは棄却法で採択か棄却かを判断する値を [0,2L×n) の区間で扱うことにあります。具体的には、m=r×n とし、この m の下位 L ビットの符号なし整数値 l が

• l≥n の場合は採択する
• l<n の場合は t=(2L−n)modn を計算したのちに、
  • l≥t であれば採択する
  • l<t であれば棄却し、l≥t となるまで r を再生成して m,l を計算し直す

という操作をします。すなわち、最初に生成された r から結果的に求まる l が n 以上であれば、剰余演算を必要とせずに採択が確定するわけです。 またいずれの状況においても、採択された m から m >> L として、目的の r′ が得られます。

なおこのアルゴリズムを実現するために、より具体的には m を表現するために 22L の精度の整数型が扱えることが前提となります。Java で言えば、int 型の乱数を生成するために long 型が必要となることに相当します。

ここで、nearly divisionless アルゴリズムをより理解するための具体例として、再び L=3, n=3 の場合を考えてみましょう。

l≥n すなわち l≥3 であれば、剰余演算を要する t の計算なしに採択が決まります。一方で t=(23−3)mod3=2 となることから、m の下位 L ビット l が 2 未満の場合に棄却となることがわかります。これを図で表現すると以下のようになります (灰色の領域が剰余演算が必要でかつ棄却となるケース、緑の領域が剰余演算なしに採択となるケース、黄色の領域が剰余演算が必要となるが採択となるケースを表します)。

最初に生成した乱数 r が 1, 2, 4, 5, 7 のいずれかであれば、r′ は剰余演算なしにそれぞれ 0, 0, 1, 1, 2 と確定します。また r が 0, 3, 6 の場合は、剰余演算を用いて t が計算され、さらに 0, 3 は棄却、6 は採択となります。

Java による nearly divisionless アルゴリズム実装Permalink

続いて、nearly divisionless のアルゴリズムを Java で実装する方法について考えていきます。以下は論文にある C++ のサンプルコードになります。

uint64_t nearlydivisionless ( uint64_t s, uint64_t (* random64 ) ( void ) ) {
  uint64_t x = random64 () ;
  __uint128_t m = ( __uint128_t ) x * ( __uint128_t ) s;
  uint64_t l = ( uint64_t ) m;
  if (l < s) {
    uint64_t t = -s % s;
    while (l < t) {
      x = random64 () ;
      m = ( __uint128_t ) x * ( __uint128_t ) s;
      l = ( uint64_t ) m;
    }
  }
  return m >> 64;
}

これをベースに Java 実装をする上でまず問題になるのが、

• Java にはプリミティブな 128 ビットの整数型が存在しない
  • 64 ビット整数型の乱数を生成しようとすると必要になる
• Java には符号なし整数を表現する型がない

この二点です。ただこればかりは言語仕様上致し方ないので、

• 32 ビット整数型の乱数を生成することに留める
  • 64 ビットの整数型があれば事足りる
• 最上位ビットをケアしながら、符号ありの整数型 int / long で表現をする
  • int で収まる整数値であっても、積極的に long 型で表現する
  • 右ビットシフトをする際は、符号なし右ビットシフト演算子 >>> を用いる

という頑張りをします。

また、Java の乱数生成メソッド Random#nextInt() は [−231,231−1] の値を返すわけなので、後続の処理を容易にするために最上位 or 最下位ビットを捨てた 31 ビットだけを使うという方法もあります。しかし、ここは余すことなく 32 ビットすべてを使うために Random#nextInt() の戻り値を long で表現することにします。これにより、JDK の Random#nextInt(int bound) の実装と比較して棄却率を低く抑えられるようになります。

結果として、fast-rng における nearly divisionless アルゴリズムの実装は以下のようになっています。

public static int nextInt(Random random, int bound) {
    if (bound <= 0) {
        throw new IllegalArgumentException("bound must be positive");
    }

    long x = ((long) random.nextInt()) & 0xffff_ffffL;
    long m = x * bound;
    long l = m & 0xffff_ffffL;

    if (l < bound) {
        for (long t = 0x1_0000_0000L % bound; l < t; ) {
            x = ((long) random.nextInt()) & 0xffff_ffffL;
            m = x * bound;
            l = m & 0xffff_ffffL;
        }
    }

    return (int) (m >>> 32);
}

おわりにPermalink

Random#nextInt(int bound) を直接利用する機会はあまりないかもしれませんが、例えば Collections#shuffle(List) の実装など、意外なところで使われていることがあります。もし Random#nextInt(int bound) 相当の処理を必要としていて、少しでも高速な実装が欲しいということであれば、nearly divisionless アルゴリズムの利用を検討してみるのもよいのではないでしょうか。